 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Интегрирование элементарных дробей
Интегрирование дробей вида (3) не представляет трудности. При 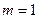
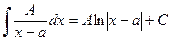
на каждом из интервалов  . Если
. Если  и
и 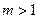 , то
, то
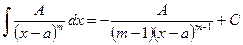
на каждом из интервалов  .
.
Рассмотрим теперь элементарные дроби вида (4)
 , где
, где  .
.
Для первого интеграла правой части имеем  при
при 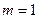 и
и  при
при 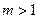 . Остаётся вычислить интеграл
. Остаётся вычислить интеграл  при
при  . Обозначим через
. Обозначим через  первообразную функции
первообразную функции  , принимающую в точке
, принимающую в точке  значение 0. Интегрируя по частям, получаем
значение 0. Интегрируя по частям, получаем
 ,
,
где  – какая-либо первообразная функции
– какая-либо первообразная функции  . Но
. Но
 ,
,
и в качестве  можно взять
можно взять  . Значит
. Значит
 ,
,
откуда при некотором  будет выполняться равенство
будет выполняться равенство
 .
.
Подставляя  , находим, что
, находим, что  , а тогда
, а тогда
 (5)
(5)
Так как  , то
, то  . Используя равенство (5) можно определить
. Используя равенство (5) можно определить  при любом натуральном
при любом натуральном  , а тем самым и
, а тем самым и  для любого натурального
для любого натурального  .
.
Таким образом, интеграл от рациональной функции вычисляется эффективно и результатом интегрирования является сумма, которая возможно включает рациональную, логарифмическую функцию и арктангенс.
Поиск по сайту: