 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Интегрирование рациональной функции
Рациональной функцией называется отношение двух многочленов. Эта функция определена на всей числовой прямой, исключая нули знаменателя, и непрерывна в каждой точке своей области определения. Наша цель– научиться интегрировать рациональную функцию на  , содержащемся в её области определения.
, содержащемся в её области определения.
Пусть 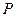 и
и  – многочлены,
– многочлены,  . Как известно,
. Как известно, 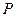 можно единственным образом представить в виде
можно единственным образом представить в виде  , где
, где  и
и 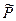 многочлены, и степень многочлена
многочлены, и степень многочлена 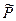 меньше степени многочлена
меньше степени многочлена  . Тем самым
. Тем самым
 .
.
Рациональная функция  есть отношение двух многочленов, причём степень числителя меньше степени знаменателя. Такую рациональную функцию мы будем называть правильной дробью. Интегрировать многочлены мы умеем. Если мы научимся интегрировать правильные дроби, то мы сможем проинтегрировать рациональную функцию.
есть отношение двух многочленов, причём степень числителя меньше степени знаменателя. Такую рациональную функцию мы будем называть правильной дробью. Интегрировать многочлены мы умеем. Если мы научимся интегрировать правильные дроби, то мы сможем проинтегрировать рациональную функцию.
Поиск по сайту: