Алгебраическое интерполирование функции

Пусть на отрезке рассматривается функция 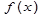, у которой известны значения в узлах интерполяции. Рассмотрим многочлен ^n.

Если перейти к введенным выше обозначениям то в этой постановке задачи рассматривается Чебышевская система функций вида

Коэффициенты этого многочлена могут быть найдены из условия совпадения в узлах интерполяции значений функций 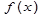с многочленом .

; *

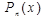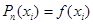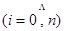Эти равенства дают систему линейных уравнений, определитель которой отличен от 0 для всех различных между собой значений .

Следовательно алгебраический многочлен 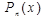для интерполяции существует и является единственным. (Единственным с точностью до формы записи) Из системы уравнений (*) видно, что коэффициенты 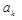линейно зависят от 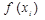по этому и многочлен 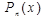линейно зависит от 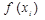и следовательно может быть представлен в виде.

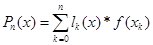
В этом выражении 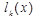нужно найти. Сделать то можно из простых алгебраических соображений.

Потребуем, чтобы функция 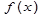и многочлен 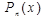обладали следующими свойствами:

1.

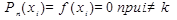
2.

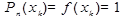
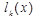это многочлен степени n для которого все узлы все узлы являются корнями этого многочлена. Все эти корни должны быть однократными т. к. их количество совпадает со степенью многочлены. Если известны корни многочлены 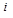, можно записать разложением многочлена на множители.

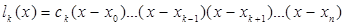
Постоянные коэффициенты 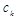могут быть определены из условия что и далее это приводит к выражению

Для компактности записи вводится многочлен в степени связанный с расположением узлов интерполяции. Которые являются для него корнями первой степени.

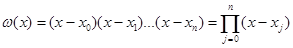
Интерполяционный многочлен Логранжа.

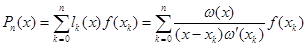
Поиск по сайту: