Интерполяционные формулы Ньютона

Рассмотри таблицы с произвольным шагом и введем понятие разделенных разностей (РР).

Разделенная разность 1ого порядка.

;

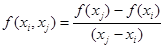Разделенная разность 2ого порядка

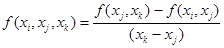
Таким образом разделенные разности любого порядка определяются по разделенным разностям n-ого порядка.

Запишем выражение для разделенных разностей через значения в узлах.

Вывод: разделенная разность является симметрической функцией узлов и имеют размерности производных функций.

;

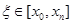
Обратимся к многочлену в степени 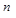. Что представляют собой их разделенные разности?

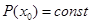; – многочлен обращается в 0 при , т. е. Делящийся 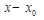безостатка.

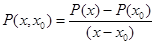
Аналогично разделенная разность 2ого порядка есть многочлен 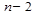степени, т. к. числитель обращается в 0 при 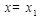. И т. д. Продолжая эти рассуждения получим, что разделенная разность 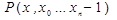есть многочлен нулевой степени, или константа. А разделенные разности более высоких порядков тождественно равны 0.

Когда 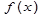– многочлен, и первый аргумент = x, можно записать рекуррентное соотношение для разделенных разностей.

;

Эта цепочка соотношений конечна. Т. к. разделенная разность n+1 порядка для многочлена n порядка тождественно равна 0. Подставляя последовательно эти соотношения друг в друга получим формулу

По этому многочлен n-ой степени выражается с помощью разделенных разностей через свои значения в узлах . Но значения интерполяционного многочлена в узлах, совпадают со значениями искомой функции, по этому и их разделенные разности совпадают. Подставив в формулу разделенные разности искомой функции, получим интерполяционную формулу Ньютона для таблиц с произвольным шагом.

Поиск по сайту: