АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Аналитическая запись логической формулы КЦУ

Читайте также:
  1. I. Определение основной и дополнительной зарплаты работников ведется с учетом рабочих, предусмотренных технологической картой.
  2. I. Расчет производительности технологической линии
  3. II. Приготовление мазка крови для подсчета лейкоцитарной формулы
  4. III. Анализ результатов психологического анализа 1 и 2 периодов деятельности привел к следующему пониманию обобщенной структуры состояния психологической готовности.
  5. Аксиология в истории методологической мысли
  6. Аналитическая геометрия
  7. Аналитическая Групповая Психотерапия
  8. Аналитическая деятельность командира по анализу и оценке морально-психологических состояний военнослужащих
  9. Аналитическая основа государственного регулирования кризисных ситуаций
  10. Аналитическая оценка решения о принятии дополнительного заказа по цене ниже себестоимости продукции
  11. Аналитическая поточная карта

Запись в форме СДНФ (Совершенная дизъюнктивная нормальная форма).

В СДНФ логическая формула представляет собой логическую сумму нескольких логических произведений, в каждое из которых входят все независимые переменные с отрицанием или без него.

Формула получается в два этапа:

а) Записывается логическая сумма произведений, в каждое из которых входят все независимые переменные. Количество слагаемых равно числу наборов таблицы истинности, на которых логическая функция равна «1»;

б) ставится знак инверсии над теми независимыми переменными, которые равны «0» в рассматриваемом наборе.

Запись в форме СКНФ (Совершенная конъюнктивная нормальная форма).

В СКНФ формула представляет собой логическое произведение нескольких логических сумм, в каждую из которых все независимые переменные с отрицанием или без него.

Как и в предыдущем случае, формула получается в два этапа:

а) Записывается логическое произведение всех сомножителей; количество сомножителей равно числу наборов таблицы истинности, на которых логическая функция равна «0»;

б) ставится знак инверсии над теми независимыми переменными, которые равны «1» в рассматриваемом наборе.

Структурные формулы в виде СДНФ и СКНФ эквивалентны и, с помощью законов алгебры, логики могут быть преобразованы одна в другую.

Пример: Синтезировать мажоритарный логический элемент на три входа.

Мажоритарным называется логический элемент, выходное состояние которого совпадает с большинством входных сигналов.

На основании данного словесного описания мажоритарного элемента составлена его таблица истинности (Таблица 5).

Таблица 5 - Таблица истинности мажоритарного элемента

X1 X2 X3 Y
       
       
       
       
       
       
       
       

На основе таблицы истинности записывается СДНФ или СКНФ функции, а затем составляется функциональная схема элемента.

СДНФ: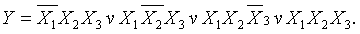

СКНФ: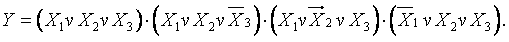

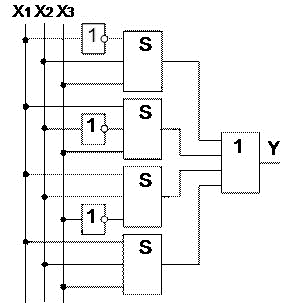
Рисунок 3 Функциональная схема мажоритарного элемента

Функциональная схема элемента, составленная на основе функции СДНФ мажоритарного элемента, приведена на рисунке 3. Схема состоит из 8 элементов, имеющих общее количество входов 19. Количество входов характеризует сложность схемы и называется «Число по Квайну». Схема составленная на основе функции СКНФ, также будет иметь 19 входов.


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)