АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Аналитическая геометрия. 1. Найдите расстояние от точки до плоскости, проходящей через точки , если (-3,4,-7),

Читайте также:
  1. Аналитическая Групповая Психотерапия
  2. Аналитическая деятельность командира по анализу и оценке морально-психологических состояний военнослужащих
  3. Аналитическая запись логической формулы КЦУ
  4. Аналитическая основа государственного регулирования кризисных ситуаций
  5. Аналитическая оценка решения о принятии дополнительного заказа по цене ниже себестоимости продукции
  6. Аналитическая психология
  7. Аналитическая работа при выборе и обосновании стратегии развития предприятии
  8. АНАЛИТИЧЕСКАЯ РАДИОКОРРЕСПОНДЕНЦИЯ
  9. Аналитическая теория личности
  10. АНАЛИТИЧЕСКАЯ ФИЛОСОФИЯ.
  11. Аналитическая философия: Л.Витгенштейн

1. Найдите расстояние от точки до плоскости, проходящей через точки 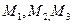, если 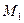(-3,4,-7), (1,5,-4), 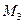(-5,-2,0), 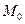(-12,7,-1).

2. Напишите уравнение плоскости, проходящей через точку A (1,0,-2)перпендикулярно вектору 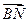, если известны координаты точек B (2,-1,3), C (0,-3,2).

3. Найдите угол между плоскостями x – 3 y + 5 = 0 и 2 x – y + 5 z – 16 = 0.

4. Найдите координаты точки A (0,0, z), равноудаленной от точек B (5,1,0) и
C (0,2,3).

5. Напишите каноническое уравнение прямой, по которой пересекаются плоскости 2 x + y + z – 2 = 0 и 2 x – y – 3 z + 6 = 0.

6. Найдите точку пересечения прямой и плоскости

x +2 y +3 z -14 = 0.

7. Установите, какую кривую второго порядка определяет уравнение
4 +3 – 8 x + 12 y – 32 = 0. Найдите для эллипса и гиперболы координаты центра, полуоси, эксцентриситет и уравнения директрис, для параболы – координаты вершины и величину параметра .

8. Найдите точки пересечения поверхности и прямой 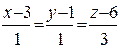. Укажите тип поверхности.


1 | 2 | 3 | 4 | 5 | 6 | 7 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.004 сек.)