 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Дз № 2. Прямая и плоскость
| № п/п | № по Еф. | Задание | Ответ | ||||||||||
| 1.180 а | Заданы плоскость  и точка и точка  . Написать уравнение плоскости . Написать уравнение плоскости  , проходящей через точку , проходящей через точку  параллельно плоскости параллельно плоскости  , и вычислить расстояние , и вычислить расстояние  , если , если   , ,  . .
|  
| |||||||||||
| 1. 1.181 а | Написать уравнение плоскости  , проходящей через заданные точки , проходящей через заданные точки  и и  перпендикулярно заданной плоскости перпендикулярно заданной плоскости  , если , если   , , 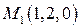 , ,  . .
| 
| |||||||||||
| 1.184 а | Написать уравнение плоскости, проходящей через три заданные точки  , ,  и и  , если , если 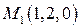 , ,  , ,  . .
| 
| |||||||||||
| 1.185 | Исследуйте взаимное расположение плоскостей   , ,   . Если плоскости параллельны, найдите расстояние между ними, если они пересекаются по некоторой прямой, то найдите косинус угла между плоскостями. . Если плоскости параллельны, найдите расстояние между ними, если они пересекаются по некоторой прямой, то найдите косинус угла между плоскостями.
| Пересекаются, 
| |||||||||||
| 1.186 | Исследуйте взаимное расположение плоскостей   , ,  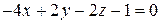 . Если плоскости параллельны, найдите расстояние между ними, если они пересекаются по некоторой прямой, то найдите косинус угла между плоскостями. . Если плоскости параллельны, найдите расстояние между ними, если они пересекаются по некоторой прямой, то найдите косинус угла между плоскостями.
| Параллельны, 
| |||||||||||
| 1.189 | Вычислить объем пирамиды, ограниченной плоскостью  : :  и координатными плоскостями. и координатными плоскостями.
| ||||||||||||
| 1.192 б | Написать уравнения плоскостей, делящих пополам двугранные углы, образованные плоскостями  и и  , если , если   , ,  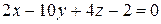 . .
| 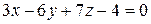 и и 
| |||||||||||
| 1.196 | Составить уравнение плоскости, проходящей через точку  и перпендикулярной к плоскостям и перпендикулярной к плоскостям  и и 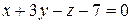 . .
| 
| |||||||||||
| 1.198 | Написать канонические уравнения прямой, проходящей через точку  параллельно: а) вектору параллельно: а) вектору  ; б) прямой ; б) прямой  ; в) оси Ох; г) оси Оz; д) прямой ; в) оси Ох; г) оси Оz; д) прямой  ; е) прямой ; е) прямой 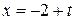 , ,  , ,  . .
| а) 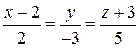 , б) , б)  , в) , в)  , г) , г)  , д) , д)  , е) , е)  . .
| |||||||||||
| 1.200 | Заданы прямая  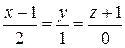 и точка и точка  (проверить!). Требуется: а) написать уравнение плоскости, проходящей через прямую (проверить!). Требуется: а) написать уравнение плоскости, проходящей через прямую  и точку и точку  ; б) написать уравнение плоскости, проходящей через точку ; б) написать уравнение плоскости, проходящей через точку  перпендикулярно прямой перпендикулярно прямой  ; в) написать уравнения перпендикуляра, опущенного из точки ; в) написать уравнения перпендикуляра, опущенного из точки  на прямую на прямую  ; г) вычислить расстояние ; г) вычислить расстояние  ; д) найти проекцию точки ; д) найти проекцию точки  на прямой на прямой  . .
| а)  , б) , б)  , в) , в)  или или  , г) , г)  , д) , д)  . .
| |||||||||||
| 1.201 | Заданы плоскость   и прямая и прямая  : :  , причем , причем  (проверить!). Требуется: а) вычислить (проверить!). Требуется: а) вычислить  и координаты точки пересечения прямой и плоскости; б) написать уравнение плоскости, проходящей через прямую и координаты точки пересечения прямой и плоскости; б) написать уравнение плоскости, проходящей через прямую  перпендикулярно к плоскости перпендикулярно к плоскости  ; в) написать уравнения проекций прямой ; в) написать уравнения проекций прямой  на плоскость на плоскость  . .
| а)  , ,  ,
б) ,
б)  ,
в) ,
в) 
| |||||||||||
| 1.202 | Пусть заданы две прямые:   и и   . Доказать, что прямые . Доказать, что прямые  и и  лежат в одной плоскости в том и только в том случае, если выполнено условие лежат в одной плоскости в том и только в том случае, если выполнено условие 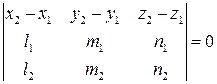 . .
| ||||||||||||
| 1.208 | При каком значении  плоскость плоскость  будет параллельна прямой будет параллельна прямой  . .
| -11 | |||||||||||
| 1.209 | Найти уравнения проекции прямой  на плоскость на плоскость  . .
| 
| |||||||||||
| 1.214 г | Написать уравнения общего перпендикуляра к прямым  и и  . .   и и   . .
| 
| |||||||||||
Поиск по сайту: