АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

ДОМАШНИЕ ЗАДАНИЯ. (денна форма навчання)

Читайте также:
  1. I. Ситуационные задачи и тестовые задания.
  2. II. Расчетная часть задания
  3. III. Задания для самостоятельной работы по изучаемой теме.
  4. III. Задания для самостоятельной работы по изучаемой теме.
  5. III. Задания для самостоятельной работы по изучаемой теме.
  6. III. Задания для самостоятельной работы по изучаемой теме.
  7. III. Задания для самостоятельной работы по изучаемой теме.
  8. III. Задания для самостоятельной работы по изучаемой теме.
  9. XI. Проанализируйте психокоррекционные возможности следующего психотехнического задания'.
  10. XI. Тестовые задания
  11. В заданиях 1-8 вычислить значение определенного интеграла.
  12. В. Защита выполненного задания у преподавателя ведущего практические занятия.

(денна форма навчання)

 

доцент: Сукач Т.Н.

 

 

Алчевськ 2012


1. Решить систему линейных алгебраических уравнений:

· Методом Крамера; Методом Гаусса; Матричным методом.

1) 2)
3) 4)
5) 6)
7) 8)
9) 10)
11) 12)
13) 14)
15) 16)
17) 18)
19) 20)
21) 22)
23) 24)
25) 26)
27) 28)
29) 30)

 

2. Найти фундаментальную систему решений и общее решение системы уравнений:

1) 2)
3) 4)
5) 6)
7) 8)
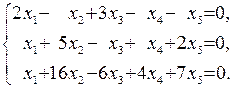
9) 10)
11) 12)
13) 14)
15) 16)
17) 18)
19) 20)
21) 22)
23) 24)
25) 26)
27) 28)
29) 30)

 

3. Даны три силы , , , приложенные к одной точке. Вычислить работу равно-действующей силы, когда ее точка приложения перемещается из точки В в точку С.

№ В С
  2,-1, 3 1, 2, 0 -1, 0, 0 1, 1, 1 2, 1, 1
  1, 2, 0 -1, 0,-1 2, 1, 2 1, 2, 3 1, 1, 1
  -1, 1, 1 2, 1, 1 1, 2, 2 1, 0, 0 2, 1,-1
  1, 0, 1 1,-2, 2 -1, 2, 1 2,-1, 0 2, 0, 1
  -1, 2, 1 0, 0, 1 0, 1, 1 3,-1, 2 1, 2, 1
  0, 1, 1 1, 2,-2 2, 1, 3 4, 2,-1 2, 1, 1
  1,-1, 1 0,-1, 1 1, 2, 1 3, 1, 2 2, 1, 0
  2, 1, 3 1, 2,-1 0,-1, 2 1,-1, 0 0, 1, 2
  2,-1, 3 2, 1,-3 -1, 2, 1 2, 0, 1 4, 2, 1
  1,-1, 3 -2, 0,-1 1, 2, 0 0, 2, 1 3, 1, 1
  1, 0, 2 -2, 0, 1 2, 1, 1 0, 0, 1 1,-1, 0
  1, 1, 0 2, 0, 0 1,-1, 2 1,-1, 1 2, 1, 1
  -1, 0, 2 2, 1,-1 1,-1, 1 2, 1, 0 1,-1, 1
  1, 1, 1 3, 2,-2 -2, 1, 0 3, 1,-2 1,-1, 2
  2,-1, 0 1,-2, 1 -1, 0, 2 2,-1, 0 2, 1, 1
  1,-1, 2 2, 1,-1 -2, 1, 1 2, 2, 1 1, 1, 1
  2, 0, 2 1,-1, 2 0,-1,-2 3, 1,-1 2, 1, 4
  2, 1, 0 1, 3,-1 -2, 1, 3 2,-1, 1 2, 1, 2
  1, 2, 3 2, 1, 1 -1, 2,-2 4, 1,-1 3, 1, 1
  1, 0,-2 1, 2, 0 1,-2, 1 3, 2, 2 2, 2, 3
  2,-1, 1 1,-1, 1 -1, 0, 0 3,-1, 1 2, 3, 1
  1, 2,-1 2,-1, 3 1,-2, 0 2,-2, 1 1, 1,-1
  3, 1, 2 1, 2,-1 2,-1, 0 1, 1, 2 2, 1, 1
  2, 1,-3 1, 2, 2 -2,-1, 3 1, 0, 2 1, 2, 1
  -2, 0, 1 1, 2, 0 -1, 2, 0 -1, 0, 1 2,-1, 1
  1, 0,-1 2,-1, 3 3, 2,-2 3, 0,-2 1, 2, 3
  0, 2, 3 3, 1, 2 0, 2, 0 2,-1, 3 3, 1, 0
  1, 2, 3 -1, 1, 1 2,-1, 3 3,-2, 1 4, 0, 2
  3, 2, 1 1,-1, 2 -1, 2, 1 2, 0,-1 3, 2,-1
  2,-1, 2 0, 2, 3 2, 0,-1 1,-2, 1 2, 2, 1

4. Вычислить площадь параллелограмма, построенного на векторах и , если:

№
     
     
     
     
     
     
     
     
     
     
     
     
     
     
     
     
     
     
     
     
     
     
     
     
     
     
     
     
     
     

 

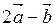
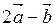
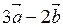
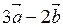
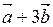
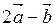
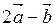
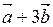
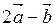
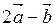
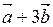
5. Даны вершины треугольника АВС. Найти: 1) длину стороны ВС; 2) уравнение ВС; 3) уравнение высоты АМ; 4) длину высоты АМ; 5) площадь треугольника АВС; 6) величину угла В; 7) координаты точки пересечения медиан треугольника.

№ А В С № А В С
  1, 1 -3,-2 3,-4   3, 0 -1,-6 -3, 1
  1,-1 -3, 1 3, 3   3, 1 -1, 4 -3,-1
  1, 2 -3,-1 0,-2   3,-1 -1, 1 0,-4
  -1, 1 -3,-2 2,-2   0, 3 6,-1 -1,-3
  -1, 2 6, 0 0,-2   0,-3 4, 6 -1,-2
  -1, 0 3, 4 6,-2   -3, 0 2, 3 6,-1
  0, 1 4, 3 6,-1   3, 4 -1, 1 2,-1
  1, 0 -3,-2 3,-3   4, 3 6,-1 1, 0
  0,-1 -6, 1 -4,-5   4,-3 1, 1 7, 2
  2, 1 -3, 0 -1,-5   -3, 4 0,-2 6, 1
  2,-1 0, 6 -5, 0   1, 0 0, 2 -1, 1
  2, 3 -2, 5 -6, 0   0, 1 -2, 0 -1,-1
  -3, 2 2, 3 6, 1   2, 1 0, 3 -1, 2
  3, 2 -2, 5 -1, 5   -1, 0 2, 2 5,-2
  -3,-2 0,-5 5, 0   0,-2 5, 2 7,-4

 

6. Даны вершины пирамиды ABCD. Найти: 1) периметр основания АВС; 2)угол между ребрами АВ и AD; 3) площадь грани АВС; 4) уравнение плоскости АВС; 5) проекцию АВ на AD; 4) объем пирамиды ABCD; 5) длину высоты пирамиды DO; 6) канонические уравнения прямой, проходящей через точку D перпендикулярно плоскости ABC.

№ A B C D
  1, 0, 0 0, 2, 1 2, 3, 4 -2, 1, 3
  2, 0, 0 1, 2, 2 -1, 1, 1 3,-1, 1
  3, 0, 0 1, 1, 1 2, 1, 0 -1, 2, 2
  -1, 0, 0 2, 1, 0 3, 2,-1 1, 1, 1
  -2, 0, 0 2, 1, 2 3,-1, 2 1, 2, 1
  -3, 0, 0 3, 1, 1 2,-1, 2 1, 2, -1
  1, 1, 0 2, 0, 1 1, 3, 0 0, 0, 4
  1, 2, 0 -2, 0, 1 0, 3, 4 3, 1, 2
  1, 3, 0 3, 1, 2 -1, 2, 1 -2, 1,-1
  1,-1, 0 2, 1, 1 -1, 2, 2 0, 0, 3
  1,-2, 0 2, 0, 0 0,-2, 1 4, 1, 2
  1,-3, 0 3, 0, 1 2, 1, 2 -1, 2, 3
  2, 1, 0 3, 2, 2 1, 0, 1 -1, 3, 3
  2, 2, 0 1, 3, 1 -1, 1, 2 3,-1, 3
  2,-2, 0 -1, 3, 4 -1, 4, 2 1,-2, 2
  -2, 1, 0 1,-1, 1 2, 2, 2 3, 0, 3
  -2,-1, 0 1, 1,-1 3, 2, 1 4, 0, 2
  2, 0, 1 3, 2, 2 -1, 1, 0 0,-1, 3
  3, 0, 1 4, 2, 2 2,-1, 1 -2, 2, 0
  1, 0, 1 2,-2, 3 0, 1, 2 3, 3, 0
  -2, 0, 1 2, 2, 2 1, 1, 3 -1, 3,-1
  -2, 0,-1 2,-1, 0 1, 1, 1 3, 4, 2
  2, 0, 2 3, 1, 1 1, 2,-1 -1, 3, 0
  3, 0, 2 2, 2, 1 4, 1, 0 -1, 4, 3
  3, 0, 4 1, 1, 3 2,-1,-1 4, 2, 1
  2, 0, 4 1, 1, 2 -1, 2, 0 0,-1, 3
  2, 0, 0 0, 0, 0 1,-1, 0 1, 1, 0
  0, 0, 1 0, 0,-2 1, 0, 0 0,-1, 1
  1, 1,-1 1, 0, 0 0, 1, 0 0, 0, 1
  0, 1,-1 1,-1, 0 2, 1,-1 3, 2, 1

 

7. Даны векторы в некотором базисе. Показать, что векторы образуют базис. Найти координаты вектора в этом базисе.

№
  -2, 4, 7 0, 1, 2 1, 0, 1 -1, 2, 4
  6, 2,-1 1, 3, 0 2,-1, 1 0,-1, 2
  1,-4, 4 2, 1,-1 0, 3, 2 1,-1, 1
  -9, 5, 5 4, 1, 1 2, 0,-3 -1, 2, 1
  -5,-5, 5 -2, 0, 1 1, 3,-1 0, 4, 1
  13, 2, 7 5, 1, 0 2,-1, 3 1, 0,-1
  -9, -1, 7 0, 1, 1 -2, 0, 1 3, 1, 0
  3,-3, 4 1, 0, 2 0, 1, 1 2,-1, 4
  3, 3,-1 3, 1, 0 -1, 2, 1 -1, 0, 2
  -1, 7,-4 -1, 2, 1 2, 0, 3 1, 1,-1
  6, 5,-4 1, 1, 4 0,-3, 2 2, 1,-1
  5,15, 0 1, 0, 5 -1, 3, 2 0,-1, 1
  6,-1, 7 1,-2, 0 -1, 1, 3 1, 0, 4
  2,-1,11 1, 1, 0 0, 1,-2 1, 0, 3
  11, 5,-3 1, 0, 2 -1, 0, 1 2, 5,-3
  8, 0, 5 2, 0, 1 1, 1, 0 4, 1, 2
  3, 1, 8 0, 1, 3 1, 2,-1 2, 0,-1
  8, 1,12 1, 2,-1 3, 0, 2 -1, 1, 1
  -9,-8,-3 1, 4, 1 -3, 2, 0 1,-1, 2
  -5, 9,-3 0, 1,-2 3,-1, 1 4, 1, 0
  -5, 5,6 0, 5, 1 3, 2,-1 -1, 1, 0
  8, 9, 4 1, 0, 1 0,-2, 1 1, 3, 0
  23,-4,30 2, 1, 0 1,-1, 0 -3, 2, 5
  3, 1, 3 2, 1, 0 1, 0, 1 4, 2, 1
  -1, 7, 0 0, 3, 1 1,-1, 2 2,-1, 0
  11,-1, 4 1,-1, 2 3, 2, 0 -1, 1, 1
  0,-8, 9 0,-2, 1 3, 1,-1 4, 0, 1
  -3, 2,18 1, 1, 4 -3, 0, 2 1, 2,-1
  8,-7,-13 0, 1, 5 3,-1, 2 -1, 0, 1
  2, 7, 5 1, 0, 1 1,-2, 0 0, 3, 1

 

8. Вычислить (без правила Лопиталя) границы:

1).

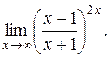
2). .

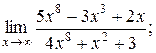
3). .

4). .

5). .

6). .

7). .

8). .

9). .

10). ; .

11).

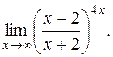
12).

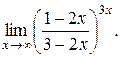
13).

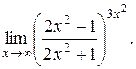
14).

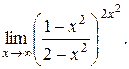
15).

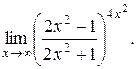
16).

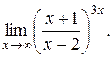
17).

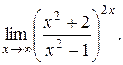
18).

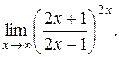
19).

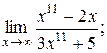
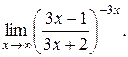
20).

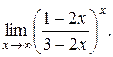
21).

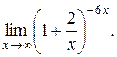
22).

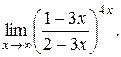
23).

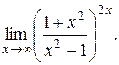
24).

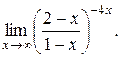
25).

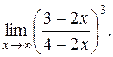
26).

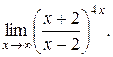
27).

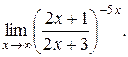
28).

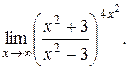
29).

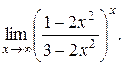
30).

 

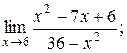
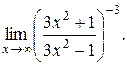
9. Исследовать на непрерывность функцию и классифицировать точки разрыва:

1). 2).
3). 4).
5). 6).
7). 8).
9). 10).
11). 12).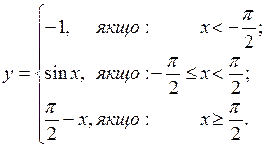
13). 14).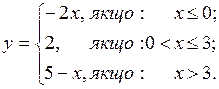
15). 16).
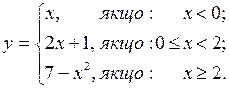
17). 18).
19). 20).
21). 22).
23). 24).
25). 26).
27). 28).
29). 30).

 

10. Найти производные данных функций:

1).

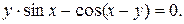
2).

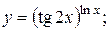
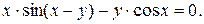
3).

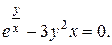
4).

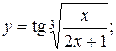
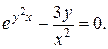
5).

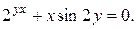
6).

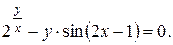
7).

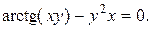
8).

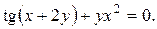
9).

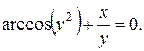
10).

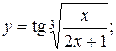
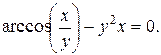
11).

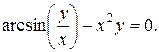
12).

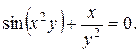
13).

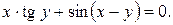
14).

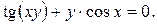
15).

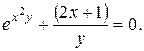
16).

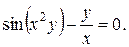
17).

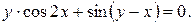
18).

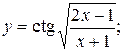
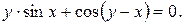
19).

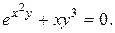
20).

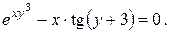
21).

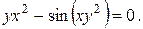
22).

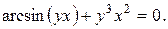
23).

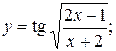
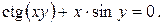
24).

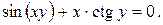
25).

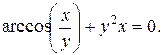
26).

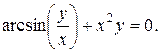
27).

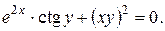
28).

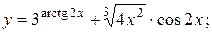
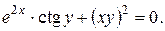
29).

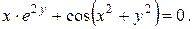
30).

 

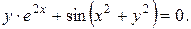
11. Провести полное исследование функций и построить их графики:

1).

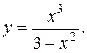
2).

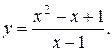
3).

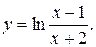
4).

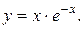
5).

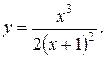
6).

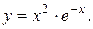
7).

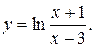
8).

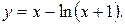
9).

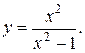
10).

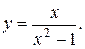
11).

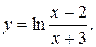
12).

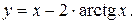
13).

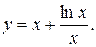
14).

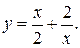
15).

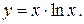
16).

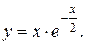
17).

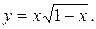
18).

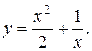
19).

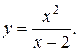
20).

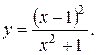
21).

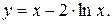
22).

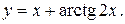
23).

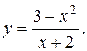
24).

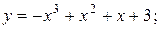
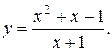
25).

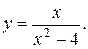
26).

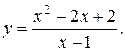
27).

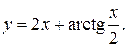
28).

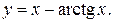
29).


1 | 2 | 3 | 4 | 5 | 6 | 7 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.05 сек.)