 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Законы и тождества алгебры логики
Математический аппарат алгебры логики позволяет преобразовать логическое выражение, заменив его равносильным с целью упрощения, сокращения числа элементов или замены элементной базы.
Законы:
1 Переместительный: X ∨ Y = Y ∨ X; X · Y = Y · X.
2 Cочетательный: X ∨ Y ∨ Z = (X ∨ Y) ∨ Z = X ∨(Y ∨ Z); X · Y · Z = (X · Y) · Z = X· (Y· Z).
3 Идемпотентности: X ∨ X = X; X · X = X.
4 Распределительный: (X ∨ Y)· Z = X· Z ∨ Y· Z.
5 Двойное отрицание:  .
.
6 Закон двойственности (Правило де Моргана): 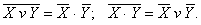
Для преобразования структурных формул применяется ряд тождеств:
X ∨ X · Y = X; X(X ∨ Y) = X — Правила поглощения.
X· Y ∨ X·  = X, (X ∨ Y)·(X ∨
= X, (X ∨ Y)·(X ∨  ) = X – Правила склеивания.
) = X – Правила склеивания.
Поиск по сайту: