 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Интерполирование (интерполяция)
|
Читайте также: |
ВычМат. Лекция (1.10.12)
Методы приближения функции.
В практике решения многих задач часто встречаются функции заданные таблицами (сеточные функции).
Интерполирование (интерполяция).
Постановка задачи.
Пусть некоторая функция известна только в узлах некоторой сетки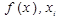 
. Эта функция заданна таблицей. Точки 
называются узлами интерполяции, а совокупность парт 
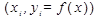Называются исходными данными для интерполяции. Теперь пусть значение аргумента 
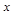отличается от узлов т. е. его нет в исходной таблице. Необходимо используя исходные данные найти 
.
Для этого необходимо получить аналитическое выражение (формулу) такую формулу, которая совпадала бы с табличными значениями в узлах сетки.
, где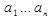 
– произвольные постоянные.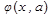 
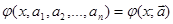
Потребовав совпадение функции с табличными значениями получим систему N уравнений.
; 
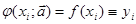Из этой системы можно определить параметры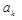 
.
Такой способ подбора параметров называется Лагранжевой интерполяцией.
Если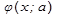 
не имеет зависимости от параметров, то интерполяция не линейная, и определение параметра 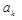может оказаться трудной задачей.
Обобщенный линейный многочлен
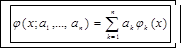
Причем все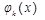 
линейно независимые функции. В этом случае система выглядит так:
;
Чтобы задача интерполяции всегда имела единственное решение надо чтобы при любом расположении не совпадающих узлов определитель системы был отличен от 0.
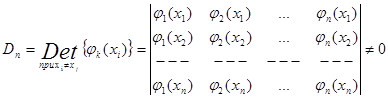
Система функций удовлетворяющих этому требованию называется Чевышевской.
Таким образом при линейной интерполяции надо строить обобщенный многочлен по какой-либо Чевышевской системе функций. Чаще всего линейную интерполяцию выполняют с помощью алгебраических многочленов.
Поиск по сайту: