АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Сравнение интерполяционных формул Лагранжа и Ньютона для таблиц с произвольным шагом

Читайте также:
  1. II. Приготовление мазка крови для подсчета лейкоцитарной формулы
  2. III. Статистические таблицы
  3. IV. Далее в этой лабораторной работе необходимо создать и сохранить запрос для отображения средних цен на все товары по таблице «Товары».
  4. IV.4. Формулярный процесс и преторская юстиция
  5. Активный запрос на создание таблицы
  6. Аналитическая запись логической формулы КЦУ
  7. Барометрическая формула
  8. Барометрическая формула. Распределение Больцмана.
  9. Безработица является неотъемлемой чертой общества с рыночной экономикой, что наглядно видно по данным таблицы 3.1.
  10. Блок завдань №1: Заповнити схеми і таблиці
  11. В таблице показана зависимость частоты генерированного переменного тока от количества магнитных полюсов и числа оборотов генератора
  12. В цьому випадку буде запропоновано вказати список таблиць і їх полів, і на підставі цих даних буде створений запит.

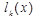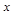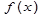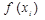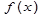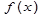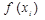В формуле Лагранжа в каждом слагаемом множитель зависит от выбора узлов и точки . И не зависит от , а сомножители позволяют учесть влияние на интерполяционный многочлен свойств функции . Эта разделенность влияния выбора узлов и свойств функции полезна при изучении сходимости интерполяционного многочлена к при 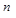стремящемся к бесконечности

 

Формула Ньютона менее удобна для таких исследований т. к. разделенные разности зависят от расположения узлов и свойств функции 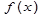достаточно сложно.

 

Однако формула Ньютона более полезна с вычислительной точки зрения. Для получения заданной точности часто интуитивно выбирают количество и расположение узлов. Если требуемая точность не достигнута, добавляют новые узла. По формуле Лагранжа надо выполнить заново (при добавлении новых узлов). А по формуле Ньютона надо добавить дополнительные слагаемые.

 

Кроме того в формуле Ньютона слагаемые располагаются в порядке убывания. И это позволяет следить о точности результата – оставляют те слагаемые, которые больше допустимой погрешности.


1 | 2 | 3 | 4 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.005 сек.)