 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Вычисление площади плоских фигур
Не вдаваясь в детали, будем считать, что все рассматриваемые ниже множества имеют площадь и объем. Изложенная выше схема позволяет в ряде случаев получить формулы для вычисления площади.
Теорема 1. Пусть  и
и 
 ,
,  .
.
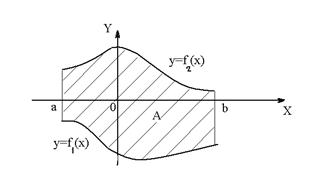
Площадь  множества А вычисляется по формуле
множества А вычисляется по формуле
 .
.
Теорема 2. Пусть  ,
,  ,
, 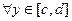 ,
,  .
.

Площадь  множества
множества  вычисляется по формуле
вычисляется по формуле
 .
.
 Множества
Множества  и
и  называются криволинейными трапециями.
называются криволинейными трапециями.
24) Вычисления объема тела по поперечным сечениям.
Будем вычислять объем тела, расположенного между двумя параллельными плоскостями 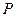 и
и  .
.

Проведем ось  перпендикулярно плоскостям
перпендикулярно плоскостям 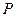 и
и  . При
. При  получаем плоскость
получаем плоскость  , при
, при  - плоскость
- плоскость 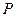 . Будем считать также, что известна
. Будем считать также, что известна  - площадь сечения тела плоскостью
- площадь сечения тела плоскостью  . Для нахождения объема тела разобьем отрезок
. Для нахождения объема тела разобьем отрезок  точками
точками  , и через точки
, и через точки  проведем плоскости, параллельные плоскостям
проведем плоскости, параллельные плоскостям 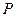 и
и  . Объем слоя, заключенного между
. Объем слоя, заключенного между  - ой и
- ой и  -ой плоскостями можно считать приближенно равным
-ой плоскостями можно считать приближенно равным  , а объем всего тела -
, а объем всего тела -  . Это приближенное значение будет тем точнее, чем меньше
. Это приближенное значение будет тем точнее, чем меньше  , поэтому объем тела
, поэтому объем тела  .
.
Из этой формулы следует принцип Кавальери: если два тела, расположенные между двумя параллельными плоскостям 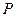 и
и  таковы, что в сечении этих тел любой плоскостью, параллельной
таковы, что в сечении этих тел любой плоскостью, параллельной 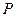 и
и  , получаются равновеликие фигуры, то и объемы этих тел равны.
, получаются равновеликие фигуры, то и объемы этих тел равны.
 Пример 1. Найдите объемправильной четырехугольной пирамиды.
Пример 1. Найдите объемправильной четырехугольной пирамиды.
Решение. Поставим пирамиду на вершину, а ось симметрии пирамиды направим по оси  . Пусть высота пирамиды равна
. Пусть высота пирамиды равна  , а основание ее, оказавшееся сверху, представляет собой квадрат со стороной
, а основание ее, оказавшееся сверху, представляет собой квадрат со стороной 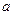 . Сечение пирамиды плоскостью на высоте
. Сечение пирамиды плоскостью на высоте  есть квадрат со стороной
есть квадрат со стороной 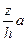 . Поэтому
. Поэтому  , и
, и  .
.
Пример 2. Определите объем цилиндрического копыта (части прямого кругового цилиндра, отсекаемого от него проходящей через диаметр основания плоскостью, образующей с основанием угол  ).
).
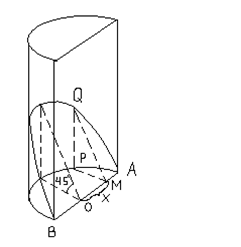 Решение. Радиус цилиндра для простоты примем равным 1. Сечение копыта плоскостью, перпендикулярной диаметру
Решение. Радиус цилиндра для простоты примем равным 1. Сечение копыта плоскостью, перпендикулярной диаметру  и удаленной оси центра на расстояние
и удаленной оси центра на расстояние  , представляет собой прямоугольный равнобедренный треугольник, катет которого равен
, представляет собой прямоугольный равнобедренный треугольник, катет которого равен  . Тогда
. Тогда  . Поэтому
. Поэтому  .
.
Поиск по сайту: