Площадь поверхности тела вращения

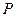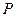Считаем известной формулу для площади поверхности усеченного конуса: . Пусть - поверхность, получаемая при вращении вокруг оси абсцисс кривой , . Площадь естественно было бы определить следующим образом. Пусть - некоторое разбиение отрезка . Для каждой пары точек , соединим отрезком прямой точки и . Тогда при вращении наряду с 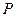получим поверхность , составленную из усеченных конусов. Ее площадь естественно считать равной .

Определение 1. Если существует конечный предел , то этот предел называется площадью поверхности .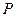

Теорема 1. Пусть . Тогда поверхность 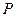имеет площадь, определяемую формулой .

Поиск по сайту: