Схема применения определенного интеграла

Пусть требуется найти значение какой-либо геометрической или физической величины , связанной с отрезком 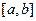изменения независимой переменной и обладающей свойством аддитивности: . Для вычисления величины можно использовать метод интегральных сумм, который заключается в следующем:

1. Подбираем функцию так, что для любого разбиения и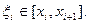

2. Пользуясь соображениями, что чем “мельче ” разбиение отрезка 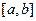, тем точнее приближенное равенство , приходим к тому, что при условии, что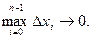

3. 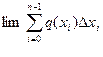при условии, что , находим как .

Пример 1 (Задача с физическим содержанием). Рассмотрим подвешенный за верхний конец прут, представляющий собой метровый кусок медной проволоки диаметром см. Спрашивается, до какой длины растянется этот кусок проволоки под влиянием собственного веса.

Решение. Растяжение проволоки связано с приложенной силой с помощью закона Гука, утверждающего, что растяжение прямо пропорционально приложенной силе и длине проволоки и обратно пропорционально площади ее сечения:

, (1)

где - постоянный множитель, зависящий от материала, из которого сделана проволока, называемый модулем Юнга. Мы не можем сразу подставить в формулу (1) вместо длины длину 100 см, а вместо - силу тяжести, легко находимую по объему прута и плотности меди, т.к. действующая на отдельные участки подвешенной проволоки сила будет разной для разных участков: если для точки подвеса эта сила действительно будет равна весу всего куска проволоки, то для второго (свободного) конца она будет равна нулю, т.к. этот конец совсем не будет нагружен. Поэтому поступим так: введем систему координат, ось которой проходит через подвешенный стержень, точка совпадет с точкой , точка - с точкой . Стержень разобьем точками , ,…, на малые участки, длины и будем считать, что в каждой точке - го участка действующая сила одна и та же: . По закону Гука растяжение - го участка стержня будет равно , а растяжение всего стержня, соответственно, . Это приближенное значение будет тем точнее, чем меньше . Следовательно, растяжение стержня .

Поиск по сайту: