Интегрирование некоторых классов функций, содержащих иррациональности

I. Интегралы вида

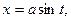
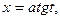
приводятся к интегралам от рациональных функций с помощью тригонометрических подстановок: соответственно для интегралов 1,2 и 3 типов.

II. Интегралы вида

подстановкой приводятся к интегралам, рассмотренным в пункте I.

III. Интегралы вида

где – действительные числа,

приводятся к интегралам от рациональных функций с помощью подстановки где – наименьшее общее краткое чисел

IV. Интегралы вида

называются интегралами от биномиальных дифференциалов. Как показано П.Л.Чебышевым они берутся лишь в случаях, когда одно из чисел , является целым.

При этом применяются следующие подстановки:

1) если - целое число, то используется подстановка , где – наименьшее общее краткое знаменателей m и n;

2) если - целое число, то использует подстановку , где -знаменатель .

3) если + - целое число, то используют подстановка , где -знаменатель .

Поиск по сайту: