Примитивная (первообразная)

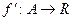Если функция дифференцируема для каждого , то операция дифференцирования ставит в соответствие функции новую функцию – производную функцию . Одна из возможных физических трактовок этой операции – определение скорости движения по функции, задающей пройденное расстояние за время движения. С точки зрения приложений естественной является обратная операция, а именно определение пройденного пути по известной скорости движения, как функции времени. Более формально, последняя операция есть операция определения функции по ее производной.

Далее буквой обозначаем одно из следующих подмножеств :

,

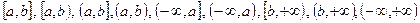где 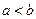. Множества такого вида мы будем называть промежутками.

Для функции положим

.

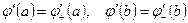Аналогичным образом определяется производная в концах промежутка , принадлежащих , во всех остальных случаях.

Определение 1. Пусть 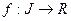. Функция называется примитивной (первообразной) функции на , если существует и .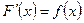

Замечание1. Из Определения 1 следует, что примитивная некоторой функции на непрерывна на .

Пример 1. Для функции 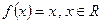, примитивной на является функция

Пример 2. Для функции 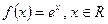примитивной на является функция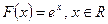

Пример 3. Для функции примитивной на является функция

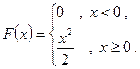
В связи с понятием первообразной возникают следующие вопросы:

1) Всякая ли функция имеет первообразную?

2) Для каких функций можно гарантировать существование первообразной?

3) Сколько первообразных может иметь одна и та же функция?

Для ответа на первый вопрос на интервале 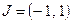рассмотрим функцию

Функция примитивной не имеет. Действительно, предположим, что такова, что 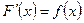для любого . По формуле конечных приращений Лагранжа .

Отсюда 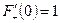. Однако 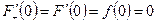. Полученное противоречие доказывает, что предположение о существование примитивной функции было неверно.

Ответ на второй вопрос дает

Теорема 1 (О существовании первообразной). Если функция непрерывна, то у нее существует первообразная.

Ответ на третий вопрос содержится в следующей теореме.

Теорема 2. Если – какая-нибудь первообразная функции , то формула

,

где – любая постоянная, дает общий вид первообразных для .

Определение 2. Совокупность всех примитивных функций функции называется неопределенным интегралом от функции и обозначается через

.

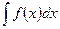Процедура определения примитивной, или неопределенного интеграла для функции , называется интегрированием .

Таблица интегралов.

Используя таблицу производных, мы можем составить таблицу некоторых интегралов. Вот эта таблица:

1. ,

2. ,

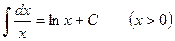3. ,

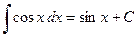4. ,

5. ,

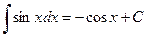6. ,

7. ,

8. ,

9. 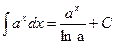(в частности ),

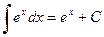10. ,

11. ( -натуральное число),

12. 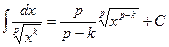( -натуральное число).

13. ,

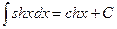14. ,

15. ,

16. .

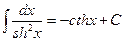Все эти формулы проверяются непосредственным дифференцированием, т. е. производная от правой части формулы всегда равна подынтегральной функции в левой части.

Отметим некоторые частные случаи формулы 1:

(, означает интеграл от подынтегральной функции, тождественно равной единице),

,

.

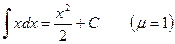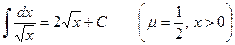Упомянем ещё и такую очевидную формулу: 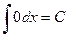, т. е. первообразные от функции, тождественно равной 0, суть постоянные.

Теперь дадим одно существенное дополнение к формуле 2. Функция непрерывна как и в интервале 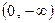, так и в интервале 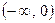. Однако формула 2 в том виде, как это записано выше, имеет смысл только при 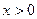. Оказывается, что если ей придать вид

2'. ,

то она будет справедливой в обоих промежутках 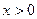и . Действительно, при 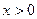формула 2' совпадает с табличной формулой 2. Если же , то 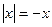, и непосредственной проверкой, с помощью правила дифференцирования сложной функции, находим, что

.

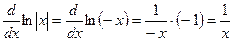Поиск по сайту: