Формула замены переменной в определенном интеграле

Теорема 1. Пусть

1. ;

2. ;

3. , т.е. .

Тогда

.

Пример 1. Найти (a>0).

Решение. Пусть , . Так как для , то .

По Теореме 1

.

Пример 2. Можно ли интеграл

вычислить с помощью подстановки ?

Решение. Нет нельзя. Как бы мы не подбирали отрезок , никогда не примет значение 2.

Пример 3. Докажите, что для непрерывной функции :

1) , если функция четная.

2) , если функция нечетная.

Решение. 1) По свойству аддитивности интеграла

Пологая , x = -t имеем

Поэтому .

2) Рассуждая так же, как в 1), имеем

.

Пример 4. Докажите, что если непрерывная периодическая функция с периодом Т, то

,

где а - произвольное действительное число

Решение. Так как , то

.

Пусть 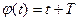. Тогда . Поэтому

. Следовательно .

Поиск по сайту: