Движение тела переменной массы

Масса тела во время его движения не всегда остаётся постоянной. Примером движения тела переменной массы может служить ракета, когда продукты сгорания запасённого в ней топлива выбрасываются через сопло двигателя и масса ракеты постепенно уменьшается.

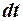Изменение импульса системы за малое время при её поступательном движении, когда масса тела изменяется за счёт отделяющихся от него или присоединяющихся к нему частиц, будет равно:

где и 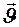- масса и скорость тела в момент времен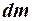и ; и - их изменения за малый промежуток времени 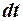; - скорость отделяющихся или присоединяющихся частиц.

Выполним преобразования и учтём, что произведение является слагаемым второго порядка малости, т. е.

или

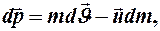
где - скорость отделяющихся или присоединяющихся частиц по отношению к телу переменной массы, т. е. относительная скорость этих частиц.

Подставим последнее выражение в уравнение (4):

- уравнение Мещерского.

В этом уравнении выражение называется реактивной силой. Она характеризует механическое действие отделяющихся или присоединяющихся частиц на тело переменной массы (например, действие на ракету вытекающей из неё струи газов).

Рассмотрим движение ракеты в отсутствии внешних сил, т. е. при . Тогда уравнение Мещерского даст

,

где - скорость истечения продуктов сгорания из сопла ракеты относительно самой ракеты. Если начальная скорость ракеты ноль, а траектория - прямая линия, то скорост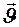и и направлены в противоположные стороны. С учётом этого получим:

или

Если - стартовая масса ракеты; - масса ракеты после окончания работы двигателя; - масса сожжённого топлива, то максимальная скорость ракеты будет:

или .

Последнее выражение носит название формула Циолковского, а скорость называется характеристическая скорость ракеты.

Реально скорость ракеты всегда меньше характеристической из-за тяготения к Земле и аэродинамического сопротивления атмосферы.

Поиск по сайту: