 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Момент силы и момент импульса относительно неподвижной точки и оси
|
Для характеристики внешнего механического воздействия на тело при его вращательном движении введём понятие момент силы.
Момент силы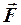 
, действующей на материальную точку А (рис. 1), относительно неподвижной т. О (полюс) есть вектор 
, определяемый векторным произведением векторов 
и 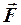(рис. 1), т. е.
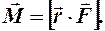
Модуль этого вектора 
, где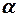 
- угол между векторами и ;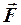 
- плечо силы, т. е. длина перпендикуляра ОВ, опущенного из т. О на линию действия силы (рис. 1).
Если на материальную точку действуют 
сил, то их результирующий момент относительно т. О будет
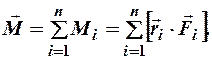
Момент импульса материальной точки относительно неподвижной т. О есть вектор 
, определяемый векторным произведением векторов 
и 
, т. е.
Если механическая система состоит из 
материальных точек (твёрдое тело, например), суммарный момент импульса системы будет:
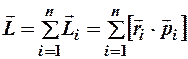. (1)
Если в качестве т. О взять т. С (центр масс), то момент сил относительно этих точек связаны между собой так:
где 
- радиус - вектор, проведённый из т. О в т. С, 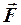- главный вектор сил системы.
Аналогичным соотношением связаны и моменты импульса системы:
Момент силы 
(или момент импульса 
) относительно неподвижной оси ОZ есть проекция на эту ось вектора (или вектора ) относительно любой точки этой оси (например, т. О).
Поиск по сайту: