АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Релятивистский закон сложения скоростей

Читайте также:
  1. B) Наличное бытие закона
  2. I. Случайные величины с дискретным законом распределения (т.е. у случайных величин конечное или счетное число значений)
  3. II закон Кирхгофа
  4. II. Законодательные акты Украины
  5. II. Законодательство об охране труда
  6. II.3. Закон как категория публичного права
  7. III. Государственный надзор и контроль за соблюдением законодательства об охране труда
  8. IX. У припущенні про розподіл ознаки по закону Пуассона обчислити теоретичні частоти, перевірити погодженість теоретичних і фактичних частот на основі критерію Ястремського.
  9. IX.3.Закономерности развития науки.
  10. А 55. ЗАКОНОМІРНОСТІ ДІЇ КОЛОГИЧЕСКИХ ФАКТОРІВ НА ЖИВІ ОРГАНІЗМИ
  11. А) Закон диалектического синтеза
  12. А) совокупность предусмотренных законодательством видов и ставок налога, принципов, форм и методов их установления.

Найдём правило пересчёта скоростей из одной СО в другую. Для начала определим связь между дифференциалами координат и времени. Из преобразования Лоренца (5) имеем:

; ; ; .

Тогда связь между проекциями скоростей на оси координат в наших СО определится выражениями

; ; .

Разделив числитель и знаменатель на , получим:

.

Обратное преобразование скоростей будет отличаться только знаком при скорости относительной СО.

Пусть частица движется вдоль оси в направлении скорости . Тогда совпадает с модулем скорости частицы 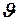в обеих СО, т. е.

(7)

Все три скорости и однонаправлены, зн. выражение (7) представляет собой закон сложения скоростей в СТО.


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.004 сек.)