АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Кинетическая энергия вращательного движения твёрдого тела

Читайте также:
  1. А — при двустороннем движении судов; б — при одностороннем движения
  2. Абсолютно упругий и неупругий удар тел. Внутренняя энергия. Общефизический закон сохранения энергии
  3. Анализ движения дебиторской и кредиторской задолженности
  4. Анализ движения денежной наличности
  5. Анализ движения денежных средств
  6. Анализ движения денежных средств прямым и косвенным методом
  7. Анализ движения и технического состояния основных средств
  8. Анализ движения основных фондов
  9. Анализ наличия и движения основных средств
  10. Анализ остатков и движения денежной наличности
  11. Анализ причин ДТП и меры, повышающие безопасность движения.
  12. Анализ случаев нарушения безопасности движения с установлением виновных и конкретных нарушений правил и порядка работы

При вращении тела вокруг неподвижной оси, момент относительно этой оси создаёт только составляющая силы , касательная к траектории точки её приложения. Поэтому элементарная работа силы 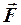будет:

Т. к. векторы 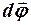и взаимно ортогональны, то Тогда

Найдём выражение кинетической энергии тела, вращающегося вокруг неподвижной оси OZ. Кинетическая энергия малого элемента этого тела, отстоящего от оси вращения на расстоянии R, равна

.

Тогда кинетическая энергия всего тела при будет:

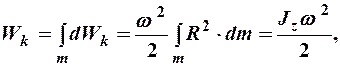
где - момент инерции всего тела относительно оси вращения .

При произвольном движении твёрдого тела его кинетическая энергия будет: ,

где 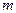- масса тела, - скорость поступательного движения его центра масс.

 


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.004 сек.)