Поле центральных сил. Потенциальные и непотенциальные силы

Силы, действующие на материальную точку, называются центральными, если они зависят только от расстояния между материальной точкой и некоторой неподвижной точкой (центром силы) и направлены всюду либо от центра сил, либо к нему. Если центр сил принять за начало координат, то выражение центральной силы будет

где - радиус - вектор, проведённый из центра сил в рассматриваемую точку поля; - проекция этой силы на радиус - вектор.

Примерами поля центральных сил могут служить гравитационное поле и электростатическое поле. Для них проекция силы обратно пропорциональна квадрату расстояния до центра силы:

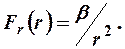
Проекции этих сил выражаются законом Всемирного тяготения Ньютона и законом Кулона соответственно:

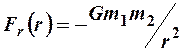- для гравитационного поля;

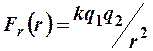- для электростатического поля,

где 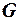и 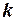- соответствующие константы. При этом 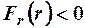для сил притяжения и 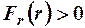для сил отталкивания.

Определим работу гравитационного поля, создавае­мого материальной точкой с массой , помещённой в т. О, при перемещении в нём материальной точки с массой 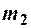из положения с радиус - вектором 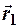в положении с радиус - вектором 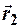(рис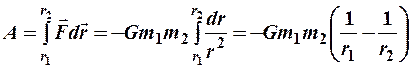. 2):

. (2)

Как видно, выражение работы в этом случае зависит только от начального и конечного положения материальной точк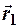и ( и 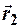) и не зависит от формы траектории и закона движения. Сила, работа которой определяется только началь­ным и конечным положением точки, называется потенциальной силой. Очевидно, что работа потенциальной силы по замкнутой траектории (контуру) будет равна нулю

Это определяется тем, что изменение направления движения точки, например, в т. 2 траектории (рис. 3) на про­тивоположное вызывает изменение знака проекции силы на радиус - вектор, что вызовет изменение знака работы. Но, т. к. 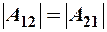, то суммарная работа по контуру будет:

.

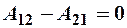Итак, работа потенциальной силы по произвольному контуру равна нулю. Математически это записывается так:

. (2)

Если силовое поле удовлетворяет условию (2), то его называют потенциальным. Т. е. поле центральных сил, как мы убедились, является потенциальным.

Существуют силы, работа которых всегда равна нулю независимо от замкнутости траектории движе­ния материальной точки. Это происходит по причине равенства нулю . Т. е. эти силы перпендику­лярны к радиус - вектору . Такие силы не принято называть потенциальными, хотя они формально удов­летворяют условию (2). Их называют гироскопическими. Примером таких сил служит сила Лоренца.

Другим примером непотенциальных сил являются диссипативные силы, которые зависят от скорости дви­жения материальных точек механической системы. Характерной их особенностью является отрицательная работа независимо от формы траектории и характера движения. Примером такой силы может быть сила трения, которая направлена всегда в сторону, противоположную вектору . Поэтому для диссипативных сил а работа отрицательна не зависимо ни от чего. Действие диссипативных сил всегда уменьшает механическую энергию системы.

Поиск по сайту: