Элементы релятивистской динамики

Релятивистский импульс. Чтобы обеспечить инвариантность закона сохранения импульса в отношении преобразований Лоренца, в определении импульса тела в ньютоновской механике

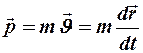
заменим время 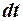собственным временем частицы 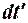, т. е. определим релятивистский импульс как

.

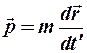Подставив сюда выражение 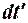, получим:

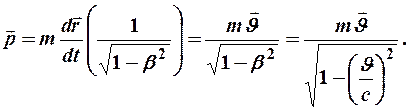
Отсюда видно, что зависимость импульса от скорости частицы 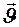является нелинейной. При получаем ньтоновский импульс . Иногда для формального совпадения выражений релятивистского и ньютоновского импульсов выражение отождествляют с понятием релятивистской массы, а под массой 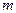понимают массу покоя тела.

Основное уравнение релятивистской динамики. Подставим полученное выражение импульса в основной закон Ньютоновской механики :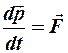

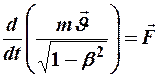. (8)

Отсюда видно, что в СТО масса утрачивает смысл коэффициента пропорциональности между ускорением и силой. В отличии от ньютоновской механики, сила не является инвариантной по отношению к инерциальной СО: в разных СО она даёт разные модули и направления. Более того, в СТО сила и ускорение как векторы не совпадают по направлению

Кинетическая энергия. Определим изменение кинетической энергии как элементарную работу внешних сил, т. е. .

Попытаемся получить это выражение из основного закона релятивистской динамики. Умножим правую часть выражения (8) на перемещение частицы 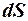, а левую - на 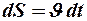. В результате получим

.

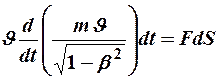Справа стоит элементарная работа , тогда слева должно быть изменение кинетической энергии частицы. Преобразуем это выражение:

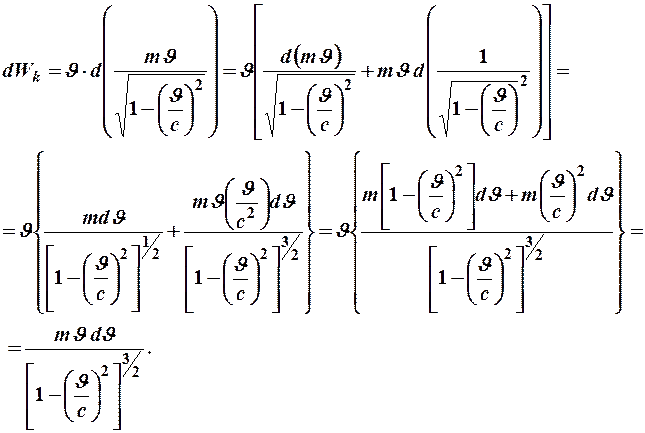
Легко убедиться, что полученное выражение является полным дифференциалом выражения .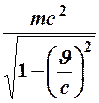

Следовательно изменение кинематической энергии будет:

,

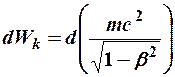а сама энергия

.

Кинетическая энергия частицы обязана равняться нулю при 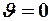. Тогда с учётом предыдущего выражения получим константу интегрирования 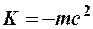. Следовательно окончательно имеем

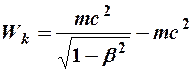. (9)

Разлагая последнее выражение в ряд Маклорена по степеням 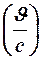, получим:

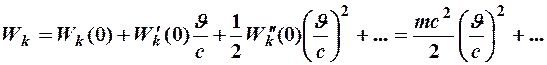
При 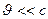остальными членами ряда можно пренебречь. В результате имеем ньютоновское выражение кинетической энергии .

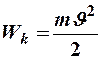Обратим внимание, что в соответствии с выражением (9) кинетическая энергия определилась как разность каких - то энергий. Выражение 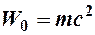называют энергией покоя частицы, а её сумму с кинетической энергией - полной энергией частицы, равной 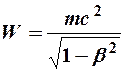. В релятивистской механики полная энергия системы сохраняется.

Поиск по сайту: