АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Закон сохранения механической энергии в консервативных и диссипативных системах

Читайте также:
  1. B) Наличное бытие закона
  2. I. Случайные величины с дискретным законом распределения (т.е. у случайных величин конечное или счетное число значений)
  3. II закон Кирхгофа
  4. II. Законодательные акты Украины
  5. II. Законодательство об охране труда
  6. II.3. Закон как категория публичного права
  7. III. Государственный надзор и контроль за соблюдением законодательства об охране труда
  8. IX. У припущенні про розподіл ознаки по закону Пуассона обчислити теоретичні частоти, перевірити погодженість теоретичних і фактичних частот на основі критерію Ястремського.
  9. IX.3.Закономерности развития науки.
  10. SCАDA-системы: основные блоки. Архивирование в SCADA-системах. Архитектура системы архивирования.
  11. А 55. ЗАКОНОМІРНОСТІ ДІЇ КОЛОГИЧЕСКИХ ФАКТОРІВ НА ЖИВІ ОРГАНІЗМИ
  12. А) Закон диалектического синтеза

Механическая энергия системы материальных точек равна сумме их кинетической энергии и потенциальной энергии взаимодействия их друг с другом и с внешними телами:

Элементарное приращение механической энергии системы за малый промежуток времени 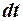будет:

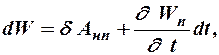
где 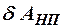- сумма работ всех действующих на систему внутренних и внешних непотенциальных сил за время .

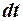Механическая система называется консервативной, если все действующие на неё непотенциальные силы не совершают работу, а все внешние потенциальные силы стационарны (не изменяются во времени). Следова­тельно для такой системы 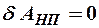и 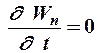Т. е. механическая энергия такой системы

, а .

Для неё справедлив закон сохранения механической энергии: при движении консервативной системы её меха­ническая энергия не изменяется.

В частности, этот закон справедлив для замкнутых консервативных систем: механическая энергия замкнутой системы не изменяется во времени, если все её внутренние силы потенциальны, а работа непотенциальных внутренних сил равна нулю.

Закон сохранения энергии связан с однородностью времени. Это свойство времени проявляется в независимости законов движения замкнутой системы от выбора начала отсчёта времени. Например, время падения тела на Земле зависит лишь от начальной скорости и высоты, но не зависит от того, в какое конкретно время это па­дение начинается.

Если система неконсервативная, то её механическая энергия будет изменяться за счёт работы внутренних потенциальных сил, т. е.

Непотенциальные силы бывают 2-х сортов: гироскопические - они работу не совершают, а зн. не могут изменить энергию; и диссипативные, работа которых приводит к уменьшению механической энергии замкнутой системы. Этот процесс называется - диссипатия энергии, а система, механическая энергия которой непрерывно уменьшается, - диссипативной системой.


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.002 сек.)