Потенциальная энергия

Потенциальной энергией системы называется часть её механической энергии, которая зависит только от конфигураций системы, т. е. от взаимного расположения всех её материальных точек и от их положения во внешнем потенциальном поле.

Убыль потенциальной энергии при перемещении системы из положения 1 в положение 2 измеряется работой внешних и внутренних потенциальных сил, действующих на эту систему, т. е.

Следовательно работа потенциальных сил при малом изменении конфигурации системы будет:

(3)

где слагаемое показывает, как изменяется потенциальная энергия за малое время 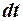при неизменной конфигурации системы (т. е. для случая нестационарных внешних потенциальных сил).

Из соотношения (3) видно, что, определяя работу , можно найти только изменение потенциальной энергии системы. Поэтому для получения однозначной зависимости потенциальной энергии от конфигурации системы необходимо выбирать в каждой конкретной задаче нулевую конфигурацию системы, т.е. как бы нуль отсчёта потенциальной энергии. Таким образом, потенциальная энергия механической системы равна работе всех потенциальных сил при переводе системы из рассматриваемого состояния в состояние нулевой конфигурации.

Рассмотрим простейшую механическую систему из одной материальной точки, на которую действует одна потенциальная сила 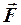. Элементарная работа этой силы с учётом (3) будет:

.

С другой стороны .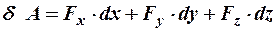

Следовательно .

Или в векторной форме

. (4)

Вектор в скобках называется градиент функции и обозначается . Поэтому краткая запись выражения (4) примет вид:

.

Часто вместо обозначения применяют оператор «набла»:

,

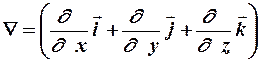т. е.

Определим потенциальную энергию материальной точки в однородном силовом поле (). Для такого поля , т. е. сила везде одинакова по модулю и направлена, например, вдоль оси Z. Такое поле будет потенциальным, т. к.

Тогда потенциальная энергия материальной точки будет

или

Например, потенциальная энергия материальной точки массы в однородном поле тяжести у поверхности Земли на высоте от её поверхности (ось Z направлена вертикально вверх):

, где .

Определим потенциальную энергию упруго деформированного тела. При такой деформации в теле возникают упругие силы, которые при продольном растяжении или сжатии определяются законом Гука: . Эта сила будет потенциальной, т. к. . Тогда потенциальная энергия с учётом (при недеформированном теле, т. е. при ) будет:

.

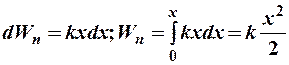Поиск по сайту: