Уравнение динамики вращательного движения твёрдого тела вокруг неподвижной оси

Возьмем произвольное твёрдого тела (система материальных точек) и направим оси декартовых координат так, чтобы ось OZ совпала с осью вращения тела, а её орт был сонаправлен с вектором угловой скорости (рис. 4). Проецируя выражение (2) на ось OZ, получим:

, (3)

Это уравнение выражает закон изменения момента импульса относительно оси OZ для нашего тела и является уравнением динамики вращательного движения твёрдого тела вокруг неподвижной оси.

Момент импульса тела относительно т. О будет

Т. к. то

Величина , равная сумме произведений масс всех материальных точек механической системы на квадраты из расстояний 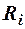до оси вращения, называется момент инерции системы материальных точек относительно этой оси.

Тогда момент импульса нашего тела как системы материальных точек относительно оси ОZ будет:

Подставим это выражение в уравнение (3):

Если тело при вращении не деформируется, то тогда, вынося 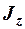из под знака производной, получим:

или

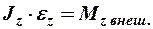, (4)

где - проекция вектора углового ускорения на ось .

Последнее выражение - это частный случай уравнения (3) при .

Поиск по сайту: