Вязкая жидкость. Стационарное движение вязкой жидкости

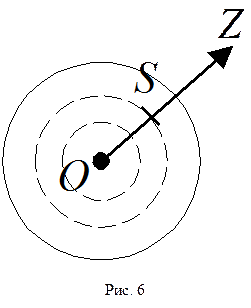
Всем реальным жидкостям и газам присуще внутреннее трение (вязкость). Рассмотрим механизм её возникновения. Возьмём круглую трубу с медленно текущей в ней жидкостью (рис. 6).

Опыт показывает, что скорость частиц жидкости изменяется от нуля вблизи трубы до максимума на её оси. Жидкость при этом оказывается как бы разделённой на тонкие цилиндрические слои, которые скользят относительно друг друга не перемешиваясь. Такое течение называется ламинарными (Lamina (лат.) - пластинка, полоска). Опыт показывает, что для стационарного течения жидкости по трубе необходимо наличие постоянной разности давление на её концах. В этом случае действие разности сил давлений компенсируется силами внутреннего трения на границе жидкости со стенкой трубы и на границах между слоями. Более быстрый слой стремится увлечь за собой медленный, действуя на него с силой 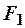, направленной по течению (рис. 7). Но более медленный слой стремится замедлить более быстрый слой, действуя на него с противоположной по направлению силой . Модуль этой силы трения определяется законом Ньютона:

,

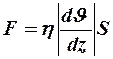где - площадь соприкосновения двух слоёв, 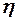- коэффициент пропорциональности, называемый динамической вязкостью жидкости. Различают ещё кинематическую вязкость В системе СИ ; .

Как отмечалось, при ламинарном течении скорость частиц жидкости изменяются от нуля до максимума. Найдём закон изменения скорости вдоль радиуса трубы. Выделим в трубе трубку тока в виде цилиндра радиуса и длиной (рис. 8). При ламинарном течении 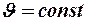, т. е. , следовательно по 2-му закону Ньютона получим:

где - результирующая сил давления слева и справа, 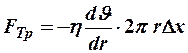- сила внутреннего трения нашей трубки (знак «-», т. к. 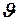убывает от центра к трубе). Следовательно

Разделив переменные, получим:

.

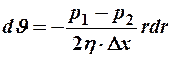Проинтегрируем это уравнение

Константу интегрирования определим из начального условия , т. е. 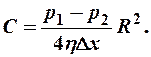Тогда будем иметь

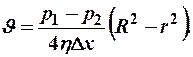
Скорость на оси трубы при 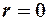будет:

(6)

С учётом этого запишем

(7)

Т. е. при ламинарном течении скорость изменяется по параболе (рис. 9). Определим объём жидкости, протекающей через поперечное сечение трубы в единицу времени (поток жидкости ).Выделим в поперечном сечении трубы кольцо радиуса и шириной (рис. 10).

Поток сквозь кольцо будет или с учётом выражения (7)

Проинтегрируем это выражение по радиусу в пределах от до

.

Подставив сюда выражение (6), получим

формула Пуазейля.

Поиск по сайту: