Преобразование Лоренца

Определим взаимосвязь координат материальной т. М с учётом постулатов СТО в абсолютной (O, X, Y, Z) и относительной СО, движущейся со скоростью вдоль оси OX (рис. 1). Очевидно, что координаты Y и Z будут связаны по-прежнему:

и .

Из рисунка видно, что т. О в абсолютной СО имеет координату X=0, а в относительной СО - Значит выражение должно обращаться в нуль одновременно с координатой . Для этого преобразование в должно иметь вид

, (1)

где - константа. На рисунке т. имеет координату в относительной СО и в абсолютной СО. Когда , то . Следовательно преобразование в должно быть вида

. (2)

По 1-му постулату Эйнштейна коэффициент должен быть одинаков в обеих СО. Теперь воспользуемся

2-м постулатом Эйнштейна. Пусть в начальный момент времени при координаты т. т. О и совпадают. В это время вдоль осей OX и посылается световой сигнал. Его вспышка в абсолютной СО

характеризуются координатами и так, что и .

Подставив это в выражение (1) и (2), получим:

Перемножим их:

или

откуда константа

,

где

Подстановка коэффициента в выражения (1) и (2) даёт

(3)

(4)

Для получения выражений преобразования времени в и назад, подставим вначале выражение (3) в (4), затем наоборот. Тогда получим:

; .

Подведём итог наших рассуждений в отношении преобразований всех координат:

; ; ; ; (5)

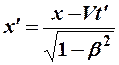; ; ; ; (6)

Эти формулы называются преобразованиями Лоренца. В них «перемешаны» координаты пространства 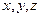и времени t, в чём проявляются взаимосвязь пространства и времени.

Причём, при преобразования Лоренца переходят в преобразования Галилея. Т. е. различие в течении времени в разных инерциальных СО связано с существованием предельной, а не бесконечной скорости распространения взаимодействий (скорость света в вакууме с).

При преобразование Лоренца и Галилея практически не отличаются, зн. преобразование Галилея сохраняют своё значение при малых скоростях.

При выражения для и становятся неопределяемыми в действительных числах, зн. движение с такой скоростью невозможно.

Поиск по сайту: