Момент инерции твёрдого тела относительно оси

Поговорим подробнее о моменте инерции тела . Из выражения (4) видно, что угловое ускорение обратно пропорционально моменту инерции 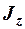, зн. момент инерции тела относительно оси является мерой его инертности при вращательном движении вокруг этой оси.

Ранее мы ввели понятие момента инерции тела как системы материальных точек. Однако масса реального тела распределена по его объёму более или менее равномерно. Поэтому момент инерции твёрдого тела в общем случае определим интегралом

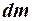где - плотность тела - масса малого элемента тела с объёмом , отстоящего от оси вращения на расстоянии R. Момент инерции тела зависит от его вещества, формы, размеров и от расположения тела относительно оси вращения.

Определение момента инерции тела относительно произвольной оси OZ облегчается использованием теоремы Штейнера, математическое выражение которой имеет вид: где - момент инерции относительно оси ОС, проходящей через центр масс (т. С) тела, 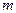- масса тела, - расстояние между параллельными осями OZ и OC.

Момент инерции однородных тел геометрически правильной формы определяется аналитически выражением (5), а для тел произвольной формы и неоднородных - экспериментально.

Рассмотрим примеры определения момента инерции.

1. Момент инерции однородного тонкостенного кругового цилиндра массы m и радиуса R относительно его геометрической оси.

Здесь ось вращения проходит через центр масс и все элементы 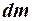цилиндра находятся на одинаковом расстоянии R от этой оси. Следовательно:

.

2. Момент инерции сплошного однородного кругового цилиндра массы m и радиуса R относительно его геометрической оси.

Разобьём наш цилиндр на большое число соосных тонкостенных цилиндров так, чтобы толщина их стенок была бы гораздо меньше радиуса любого из них (рис. 5). Возьмем какой - либо из этих цилиндров с радиусом . Его момент инерции относительно оси ОС будет:

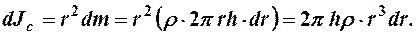
Момент инерции всего сплошного цилиндра найдём как интеграл по в пределах от О до R:

Поиск по сайту: