Уравнение движения жидкости

Различаются два типа сил, действующих на элемент объёма жидкости: массовые и поверхностные.

Массовые силы - это такие, действие которых не зависит от присутствия других частей жидкости, кроме рассматриваемого элемента. Их модуль пропорционален массе этого элемента жидкости. Например, сила тяжести. Массовая сила определяется как , где - объём рассматриваемого элемента, - плотность жидкости, - напряжённость поля массовых сил. Например, для силы тяжести 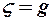- ускорение свободного падения. Массовые силы называют потенциальными, если их напряжённость можно представить в форме:

,

где - потенциал массовой силы.

Поверхностными силами называют приложенные к элементу жидкости со стороны прилегающих к нему других элементов. Поверхностная сила, отнесённая к единице поверхности элемента жидкости, называется напряжением. В состоянии равновесия жидкости касательные напряжения будут равны нулю, а поверхностные силы будут представлять лишь силы давления жидкости.

Возьмём трубку тока стационарного течения жидкости (рис. 2). По закону сохранения массы, через любое сечение трубки в единицу времени пройдёт одна и та же масса жидкости, т. е. Заменив массу через плотность и объём, получим 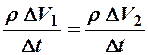или с учётом

Таким образом, для любой пары сечения трубки имеем:

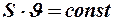или . (1)

В более общем виде полученное соотношение можно записать так:

. (2)

Выражения (1) и (2) представляют собой уравнения неразрывности жидкости.

Уравнение движения жидкости с учётом массовых и поверхностных сил примет вид:

Уравнение Эйлера (3)

где - давление жидкости;

Основной задачей механики жидкостей является отыскание полей скорости, давления и плотности жидкости, движущейся под действием внешних сил, т. е. нахождение следующих 5-ти функций координат и времени:

; ; ; ; .

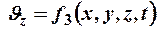Для решения этой задачи используют уравнения неразрывности и движения, а также начальные условия, т. е. значение этих 5-ти функции в момент времени .

Поиск по сайту: