Кинематическое описание движения

При движении т.М её координаты и радиус-вектор изменяются со временем. Поэтому для описания движения т.М надо указать вид функции либо всех трех её координат, либо её радиус-вектора:

или

. (3)

В системе СИ размерность .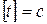

Три уравнения (2) или эквивалентное им векторное уравнение (3) называются кинематическим уравнением движения.

Траектория точки - это линия, описываемая точкой при движении относительно выбранной системы отсчета.

В зависимости от формы траектории различают прямолинейное и криволинейное движение точки.

Длина пути (путь) - это расстояние, пройденное точкой за рассматриваемое время вдоль траектории в направлении движения точки.

Пусть точка движется по криволинейной траектории АВ (рис. 2) так, что при она находится в т. A, а при находится в т. М. Если за рассматриваемое время точка двигалась только в одном направлении, то путь S(t) точки за это время будет равен дуге AM, т.е. .

Если точка за время от до дошла до т. В, а затем за оставшееся время вернулась в т. М, то путь точки за всё рассматриваемое время от до будет:

Следовательно путь .

Вектором перемещения точки за промежуток времени от до называется приращение радиус-вектора 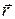за этот промежуток времени:

.

Вектор перемещения направлен вдоль хорды, стягивающей точки траектории, соответствующие временам и .

Если рассматривать достаточно малый промежуток времени , то можно пренебречь отличием модуля вектора перемещения и длиной пути , т. е. можно считать, что . Из сказанного видно, что вектор будет направлен по касательной к траектории в данной точке в сторону ее движения т.е.

,

где - единичный вектор касательной.

Вектор перемещения можно представить за конечной промежуток времени (от до + ) через векторную сумму перемещений вдоль осей координат:

Здесь

;

;

.

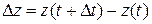Поиск по сайту: