Скорость и ускорение материальной точки

Для характеристики направления и быстроты движения точки введём понятие вектора скорости. Средней скоростью точки в промежутке времени называется вектор

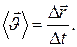
Средняя скорость направлена так же, как вектор перемещения .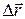

Так как

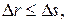
то

,

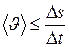где знак равенства соответствует прямолинейному движению в одном направлении.

Скорость точки в момент времени есть вектор 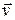, равный первой производной от радиус-вектора 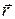этой точки по времени:

,

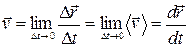причём модуль скорости v будет

.

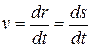В системе СИ размерность 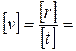м/с.

Подставляя вместо 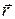его ортогональное разложение (1), получим:

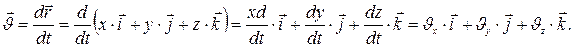
Следовательно, модуль скорости можно определить через её проекции на оси координат следующим образом:

.

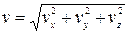При прямолинейном движении направление скорости как вектора остаётся неизменным. Движение точки называется равномерным, если модуль её скорости не изменяется со временем, т. е.

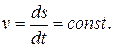
При равномерном движении точки длина пройденного пути зависит от времени линейно:

.

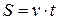В общем случае неравномерного движения пройденный путь определится как интеграл от скорости

.

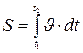Средней путевой скоростью неравномерного движения 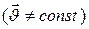точки называется скалярная величена

,

где 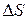- длина пройденного пути данного участка траектории. Скорость равна модулю вектора скорости такого равномерного движения, при котором на прохождение того же пути 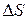потребуется столько же времени , как при неравномерном движении.

При криволинейном движении точки 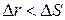. Поэтому в общем случае средняя путевая скорость 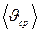не равна модулю средней скорости на том же участке траектории.

Для характеристики быстроты изменения вектора скорости при неравномерном движении точки введём понятие ускорения.

Средним ускорением точки в интервале времени от до 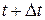называется вектор 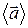, равный отношению приращения вектора скорости 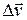за этот промежуток времени к его продолжительности :

.

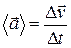Мгновенным ускорением точки называется векторная величина 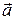равная первой производной от вектора скорости или второй производной от радиус-вектора по времени:

.

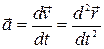Иначе, ускорение точки в момент времени есть предел среднего ускорения:

.

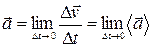В системе СИ размерность 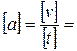м/с.

Ускорение, как радиус-вектор и скорость, можно представить в ортогональном базисе:

.

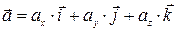Рассуждая так же, как для вектора скорости, получим проекции ускорения на оси координат:

; ; .

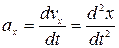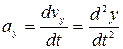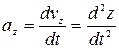Следовательно, модуль ускорения будет равен:

.

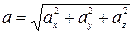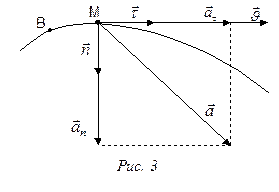
При криволинейном движении вектор ускорения 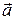направлен в сторону вогнутости траектории (рис. 3) и лежит в плоскости движения точки. В этой плоскости вектор ускорения принято разлагать на две вза­имно перпендикулярные составляющие 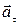и :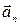

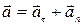
Составляющая 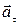называется касательным (тангенциальным) ускорением точки. Оно направлено по касательной к траектории и равно

,

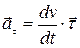а его модуль

.

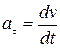Здесь 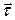- орт касательной, проведённой в данной точке по направлению вектора 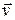(рис. 3).

Касательное ускорение характеризует быстроту изменения модуля вектора скорости точки. Если 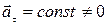, то движение называется равнопеременным. В этом случае модуль вектора скорости зависит от времени линейно:

,

где - модуль начальной скорости точки.

Путь при таком движении определиться как интеграл

.

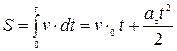Составляющая 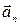называется нормальным (центростремительным) ускорением точки. Оно направлено перпендикулярно (по нормали) к касательной в данной точке траектории в сторону центра её кривизны (рис. 3). Вектор нормального ускорения равен:

,

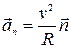а его модуль

.

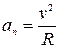Здесь 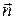- орт нормали, 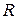- радиус кривизны траектории в данной точке.

Если точка движется прямолинейно, то 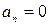и ускорение точки равно её касательному ускорению: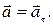

Поиск по сайту: