 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Уравнения моментов. Закон сохранения момента импульса
Продифференцируем выражение (1) по времени
Здесь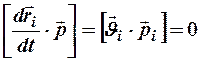 
, т. к. векторы 
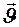и 
коллинеарны.
Тогда 
Разберёмся с суммой моментов внутренних сил. По 3-му закону Ньютона для каждой пары материальных точек системы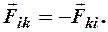 
|
Тогда их суммарный момент будет 
Но векторы 
и 
коллинеарны (рис. 2), поэтому их векторное произведение даст ноль. Следовательно
.
В результате получим
, (5)
Последнее выражение представляет закон изменения момента импульса системы относительно неподвижной точки: производная по времени от вектора 
относительно т. О есть суммарный момент всех внешних сил, действующих на систему относительно той же точки.
Если в качестве т. О взять т. С (центр масс), то выражение (2) примет вид:
.
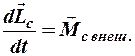Для замкнутой системы момент внешних сил равен нулю по причине равенства нулю векторной суммы этих сил. Поэтому, в соответствии с выражением (2) получим:
откуда 
откуда 
Если в качестве неподвижной т. О взять т. С (центр масс), то
; 
,
|
где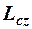 
- проекция вектора 
на ось, проходящую через т. С. Сделанные выше выводы носят название закон сохранения момента импульса: момент импульса замкнутой системы относительно неподвижной точки или неподвижной оси есть величина постоянная и неизменная во времени.
В справедливости этого закона можно убедится на примере уравновешенного гироскопа с 3-мя степенями свободы вращательного движения. Такой гироскоп - это симметричное однородное тело, быстро вращающееся относительно оси, проходящей через центр его масс (рис. 3). Три степени свободы ему обеспечивает специальный подвес. Если центр подвеса (т. О) совпадает с центром масс гироскопа (т. С), то результирующий момент силы тяжести всех его материальных точек (частей) относительно т. О будет ноль. При любых поворотах подвеса ось гироскопа ОX не изменяет своего положения в пространстве. Причина этого в том, что при вращении гироскопа вокруг своей оси симметрии, его момент импульса направлен вдоль оси ОX. Но 
(без учёта малых сил трения в осях), поэтому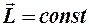 
, а зн. направление оси ОX должно не изменяться.
Гироскоп нашёл применение в гирокомпасах, в устройствах стабилизации кораблей и др. областях.
Поиск по сайту: