Следствия из преобразований Лоренца

Относительность одновременности. Пусть в абсолютной СО в двух точках с координатами и происходят два одинаковых события одновременно так, что . Найдём разность моментов времени и для этих событий в относительной СО. Если относительная СО движется со скоростью V вдоль оси ОX, то

.

Если относительная СО движется со скоростью - V вдоль оси ОХ, то

Т. е. в любой относительной СО указанные события оказываются неодновременными, причём в первом случае (скорость СО V) второе событие будет происходить раньше первого, а во втором случае (скорость СО-V) - наоборот. Ясно, что эти рассуждения относятся только к двум причинно несвязанным событиям, т. к. в любой СО нельзя «умереть» раньше, чем «родиться».

Относительность длин тел. Пусть стержень покоится в относительной СО вдоль оси , которая движется вдоль оси OX со скоростью V. Длина этого стержня в относительной СО будет . Подставим сюда координаты концов стержня и из преобразования Лоренца:

или ,

где - длина стержня в абсолютной СО, т. е. длина стержня, движущегося относительно неё со скоростью . Следовательно длина 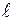тела в направлении движения будет меньше длины покоящегося тела. В направлениях, перпендикулярных движению тела его длина не изменяется, т. к. и .

Промежуток времени между событиями. Пусть в нашей относительной СО происходят два события, разделённые промежутком времени (например, начало и окончание занятий в институте). Найдём промежуток времени между этими событиями в абсолютной СО: . Подставим сюда времена и из преобразования Лоренца:

или

Время 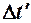, отсчитанное по часам, движущимся вместе с телом, называется собственным временем. Тело в этой СО покоится, зн. 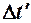будет инвариантно по отношению к любой инерциальной СО. Т. к. , то можно сказать, что движущиеся часы идут медленнее, чем покоящиеся.

Интервал между событиями - это расстояние между двумя мировыми точками в пространстве - времени, соответствующими двум событиям.

Ньютоновская механика построена на геометрии Евклида, в которой интервал между событиями (расстояние между двумя точками в трёхмерном евклидовом пространстве - его метрика) определяется как

.

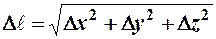В 4-х мерном пространстве - времени Минковского интервал между событиями определяется другой метрикой:

.

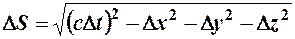Сопоставляя метрики этих пространств, запишем:

,

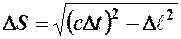где - расстояние между точками обычного пространства.

Преобразуем последнее выражение:

.

Т. к. 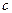-константа, а 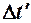- инвариантное по отношение к выбору инерциальной СО, то тоже будет инвариантным.

Поиск по сайту: