Кинематика абсолютного, относительного и переносного движения

Различают инерциальные и неинерциальные системы отсчёта (СО). Инерциальные СО либо покоятся, либо движутся прямолинейно и равномерно. Неинерциальные СО движутся с ускорением.

Абсолютным движением материальной точки называется её движение по отношению к неподвижной СО. Такую СО назовем абсолютной.

Относительным движением материальной точки называется движение по отношению к любой подвижной СО. Такую СО назовём относительной.

Переносным движением материальной точки называется абсолютное движение той точки относительной СО, через которую проходит материальная точка в данный момент времени.

Рассмотрим движение т. М в абсолютной () и относительной () СО, которая в общем случае движется поступательно относительно первой СО со скоростью и вращается относительно т. с угловой скоростью (рис. 1).

Радиус - векторы т. М в названных СО связаны между собой так:

, (1)

где распишем через орты ,

радиус - вектор, соединяющий т. т. О и .

Следовательно абсолютная скорость т. М, т. е. её скорость относительно абсолютной СО будет

. (2)

Разберёмся с каждым слагаемым выражения (2) отдельно. Первое из них есть скорость поступательного движения относительной СО. Второе слагаемое даст

. (3)

Часть выражения (3) есть относительная скорость т. М, т. е. её скорость в относительной СО.

Выясним физический смысл части II выражения (3). Т. к. изменение ортов во времени может происходить только за счёт вращения относительно СО, то часть выражения (3) есть - линейная скорость вращения той точки относительной СО, через которую в данный момент проходит т. М. Сумму линейных скоростей

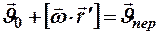(4)

называют переносной скоростью т. М.

Следовательно абсолютную скорость можно выразить следующим образом:

. (5)

Последнее выражение называют законом сложения скоростей.

Аналогичным образом разберёмся с ускорением т. М относительно наших СО.В соответствии с выражением (5), абсолютное ускорение т. М, т. е. её ускорение в абсолютной СО будет:

. (6)

Слагаемое в соответствии с частью выражения (3) даст

. (7)

Часть выражения (7) есть относительное ускорение т. М. Часть выражения (7) по изложенным ранее соображениям есть произведение .

Второе слагаемое выражения (6) в соответствии с выражением (4) даст

. (8)

Первое слагаемое 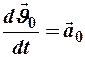есть ускорение поступательного движения т. . Второе слагаемое выражения (8) в соответствии с частью выражения (3) даст

. (9)

Часть выражения (9) представляет собой линейное ускорение вращения той точки относительной СО, через которую в данный момент проходит т. М. Это ускорение принято разлагать на две взаимно ортогональные составляющие: вращательное и осестремительное ускорения.

Суму ускорений называют переносным ускорением т. М. Часть выражение (9) полностью совпадает с частью II выражения (7), т. е. будет равна

Таким образом, абсолютное ускорение т. М можно записать так:

, (10)

где - поворотное (кориолисово) ускорение.

Заметим, что кориолисово ускорение возникает только для тех тел, которые движутся со скоростью относительно вращающихся систем отсчёта, причём так, что векторы и не направлены вдоль одной прямой.

Поиск по сайту: