Потенциальные силы

В борьбе с крестьянскими движениями император использовал преимущественно репрессивные методы, которые не приносили желаемой эффективности. В 1901 году, по инициативе начальника охранного отделения, С. Зубатова, в больших городах империи были созданы специальные профсоюзные комитеты, деятельность которых контролировалась полицией.

Такие организации должны были выступать в роли арбитров в противостояниях между рабочим классом и предпринимателями. Однако, вопреки ожиданиям правительства, члены профсоюзов, вместо внедрения в обществе «полицейского социализма», открыто становились на сторону протестующих, защищая их права и свободы.

За такой просчет, император уже в 1903году принудил Зубатова подать в отставку и в течение трех месяцев ликвидировал все профсоюзные комитеты.

3.Семья как социальный институт. Развитие семьи в современном мире.

Семью можно рассматривать как малую группу и особый социально-культурный институт, связывающий индивидов общностью быта и взаимной моральной ответственностью. Семья — древнейшая и наиболее распространенная из малых социальных групп. Ее основаниями являются совместная жизнь и хозяйство, взаимопомощь, духовное общение. Семья — фундамент общества, поскольку именно она формирует основные качества человека и вводит его в мир социальных отношений.

Потенциальные силы

В общем случае сила зависит от положения точки, ее скорости и времени:

В отдельных случаях сила может зависеть только от части своих аргументов. В частности, существует класс сил, зависящих только от положения точки в пространстве. Это значит, что известны выражения

определяющие проекции силы на координатные оси как функции координат точки.

Пространство или часть пространства, в каждой точке которых определен некоторый вектор, называется векторным полем. В зависимости от физического смысла вектора это может быть силовое поле, поле скоростей, поле ускорений и т.д. Задание силы, зависящей от положения точки, означает, что при помощи указанных равенств одновременно задается силовое поле.

Если в указанной области пространства существует функция, такая, что проекции силы F равны соответствующим частным производным этой функции

то сила F называется потенциальной силой, а функция U — силовой функцией. В задачах механики чаще используется функция которая отличается от силовой функции только знаком и называется потенциальной энергией, или потенциалом силы F. При помощи потенциальной энергии проекции потенциальной силы определяются равенствами:

Потенциальные силы обладают одним важным свойством совершаемая ими работа определяется только начальным и конечным положениями точки и не зависит от способа перемещения (формы пути, закона движения) из одного положения в другое. Действительно, вычисляя работу потенциальной силы, находим:

В этой формуле — значение потенциальной энергии в начальном положении точки; то же в конечном положении точки.

Важно заметить, что не всякая сила, зависящая от положения, является потенциальной. Для потенциальности требуется еще выполнение условий существования функции. Эти условия подробно рассматриваются в математике и сводятся к выполнению следующих трех равенств:

Пример. К стержню ОА (рис. 1) приложены три активные силы — вес стержня, упругая сила пружины F и постоянная по модулю сила Р, перпендикулярная к стержню. Определить, какие из этих сил потенциальны, а какие — нет. Жесткость пружины — с, натуральная длина пружины — а, длина стержня.

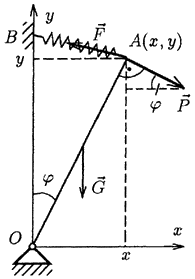
Рис. 1.

Решение. Изображаем систему в произвольном положении, вводим декартову систему координат. Все силы лежат в плоскости, поэтому из условий потенциальности силы в данном случае остается только первое равенство.

Проекции силы тяжести на выбранные оси равны:. Имеем. Следовательно, поэтому сила тяжести является потенциальной силой.

Аналогичным образом можно показать, что сила упругости пружины также является потенциальной силой.

Определяем проекции силы Р:

Находим нужные производные:

Видно, что, поэтому сила не является потенциальной. Силы такого типа иногда называют следящими силами.

Поиск по сайту: