Вычисление потенциальной энергии

При исследовании движения механической системы с потенциальными силами вместо сил часто используется потенциальная энергия. Она может быть вычислена путем интегрирования уравнения в полных дифференциалах:

Однако проще это сделать непосредственно, вычисляя работу силы.

Для этого сначала познакомимся с некоторыми новыми понятиями. Пусть потенциальная энергия силы, приложенной к точке М. Полагая

получаем уравнение поверхности в пространстве Oxyz, которая называется поверхностью уровня (рис. 46). Поверхность уровня обладает следующим свойством: при движении точки по поверхности уровня потенциальная сила не совершает работы, так как для любых двух точек, принадлежащих этой поверхности, имеем.

Рис. 46.

Придавая постоянной С различные значения, -получим семейство поверхностей (рис. 47). Все пространство оказывается как бы расслоенным поверхностями уровня. Выберем одну из них за поверхность нулевого уровня потенциальной энергии и подсчитаем работу, совершаемую потенциальной силой при перемещении точки М из данного положения в какую-либо точку, принадлежащую нулевой поверхности уровня (рис. 48).

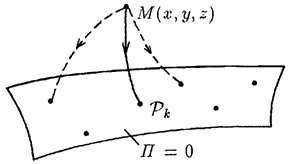
Рис. 47.

Рис. 48.

Учитывая, что, получаем

Отсюда следует формула

Тем самым устанавливается следующее правило для вычисления потенциальной энергии: чтобы вычислить потенциальную энергию в данном положении точки, достаточно вычислить работу, совершаемую силой при перемещении точки М из этого положения в какую-либо точку, принадлежащую нулевой поверхности уровня потенциальной энергии (см. рис. 48).

Пример 1. Для математического маятника (рис. 49) поверхностями уровня служат горизонтальные прямые и т. д. Любая из них может быть принята за линию нулевого уровня потенциальной энергии. Примем в качестве таковой горизонталь, проходящую через точку подвеса О. Тогда для потенциальной энергии маятника получаем

Если за начало отсчета П принять горизонталь, проходящую через положение равновесия маятника (точку), потенциальная энергия будет иметь выражение

Пример 2. Пружинный маятник состоит из массы М, прикрепленной к неподвижной стенке при помощи пружины жесткости с, имеющей натуральную длину а (рис. 50).

Рис. 49.

Поверхностями уровня в данном случае являются точки оси. Приняв за начало отсчета потенциальной энергии ее значение в положении равновесия для потенциальной энергии маятника в данном положении, определяемом координатой, будем иметь

Если за нулевой уровень принять значение потенциальной энергии в некоторой точке с координатой, то будет равна работе упругой силы пружины при переходе тела из положения М в положение. При вычислении этой работы удобно воспользоваться свойством независимости работы потенциальной силы от формы пути и переход осуществить так: вначале из положения М перейти в начало координат, далее из начала координат — в положение (см. рис. 50). В каждом из указанных переходов одно из крайних положений соответствует недеформированной пружине, и работа может быть вычислена по формуле. На участке МО пружина разгружается, при этом совершается положительная работа. При переходе пружина нагружается, и работа упругой силы отрицательна:. В итоге для потенциальной энергии получаем

На материальную точку могут действовать несколько сил, обладающих потенциалом. Тогда можно говорить также о потенциальной энергии материальной точки, понимая под ней сумму потенциальных энергий, соответствующих каждой силе. Понятие потенциальной энергии естественным образом обобщается и на случай механической системы, где принимает смысл суммы потенциальных энергий всех потенциальных сил, действующих на систему.

Рис. 50.

Рис. 51.

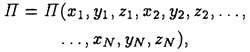
При этом потенциальная энергия в общем случае будет зависеть от координат точек системы:

Пример 3. Вычислить потенциальную энергию системы, состоящей из ползуна и прикрепленного к нему математического маятника (рис. 51). Масса ползуна — маса маятника — жесткость пружины.

Выберем систему координат, как показано на рис. 51. Ось у проходит через точку подвеса маятника А в положении равновесия системы. Вычисляем потенциальную энергию сил тяжести, приняв за нулевой уровень потенциальной энергии ось:

Для потенциальной энергии пружины, которую отсчитываем от значения при недеформированной пружине, будем иметь

Потенциальная энергия всей системы определяется выражением

Поиск по сайту: