 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Физический маятник. Цель работы: Экспериментальное определение ускорения свободного падения методом колебания физического маятника
Цель работы: Экспериментальное определение ускорения свободного падения методом колебания физического маятника. Определение момента инерции физического маятника.
Приборы и принадлежности: универсальный маятник ФП-1, секундомер, линейка.
Теоретическое введение
В теории колебаний физическим маятником называется твердое тело, укрепленное на неподвижной горизонтальной оси, не проходящей через его центр масс и способное совершать колебания относительно этой оси (рис.1).
|
Можно показать, что маятник, отклоненный на малый угол a от положения равновесия, будет совершать гармонические колебания.
Обозначим через J момент инерции маятника относительно оси О. Пусть точка С является центром масс. Силу тяжести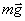 
можно разложить на две составляющие, одна из которых 
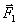уравновешивается реакцией оси. Маятник приходит в движение под действием другой составляющей 
, величина, которой:
Для малых углов sin a» a и выражение (1) запишем:
Знак минус означает, что сила направлена в сторону, противоположную отклонению маятника от положения равновесия.
Основное уравнение динамики вращательного движения для физического маятника запишется:
Момент силы относительно оси О с учетом (2):
где l – расстояние от центра масс С до оси О.
Угловое ускорение маятника:
Поставив (4) и (5) в уравнение (3), получим:
Откуда
Обозначив
получим:
По структуре уравнение (6) является дифференциальным уравнением гармонических колебаний с циклической частотой w. Период колебаний физического маятника равен:
Отсюда момент инерции физического маятника:
Величина
называется приведенной длиной физического маятника, равной длине математического маятника, имеющего тот же период колебаний, что и физический, т.е.
Точка О1, лежащая на прямой, проведенной через точку подвеса О и центр масс С, на расстоянии приведенной длины l0 от оси вращения, называется центром качания маятника (рис.1). Центр качания лежит всегда ниже центра масс. Точка подвеса О и центр качания О1сопряжены друг с другом, т.е. перенос точки подвеса в центр качания не меняет периода колебания маятника. Точка подвеса и центр качания обратимы, а расстояние между этими точками представляет собой приведенную длину l0 одного из типов физического маятника, так называемого оборотного маятника.
Обозначим через J0 момент инерции маятника относительно оси, проходящей через его центр масс. На основании теоремы Штейнера момент инерции J относительно любой оси, параллельной первой:
где m – масса маятника, l – расстояние между осями.
Тогда при подвешивании маятника за точку подвеса О период колебаний:
а при подвешивании за центр качания О1 , когда маятник находится в перевернутом положении, период: 
где l2 и l1 – расстояние между центром масс и соответствующими осями колебаний.
Из уравнений (9) и (10):
откуда:
Формула (11) остается справедливой при колебаниях маятника относительно двух произвольных осей О и О/, не обязательно сопряженных, но расположенных по разные стороны от центра масс маятника.
Поиск по сайту: