Физический маятник и его малые колебания

Физическим маятником называется твердое тело, находящееся в поле силы тяжести и имеющее горизонтальную ось вращения, не проходящую через центр тяжести тела.

Пусть — масса тела, J — его момент инерции относительно оси вращения — расстояние от центра тяжести до оси вращения (рис. 36). Выведенное из положения равновесия, тело будет вращаться либо совершать колебательное движение. В обоих случаях дифференциальное уравнение движения имеет один и тот же вид (силами трения пренебрегаем):

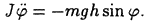
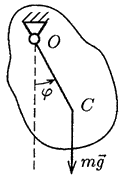
Рис. 36.

Пусть начальные условия таковы, что угол все время остается малым (максимальное отклонение от вертикали не превышает). Тогда можно приближенно принять (в радианах) и рассматривать более простое уравнение:

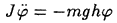
или, что то же, уравнение

Это уравнение называется дифференциальным уравнением малых колебаний физического маятника. Из него следует, что малые колебания физического маятника являются гармоническими колебаниями частоты

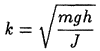
и периода

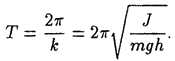
Амплитуда и фаза колебаний будут определяться начальным отклонением и начальной угловой скоростью физического маятника.

Поиск по сайту: