АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Длина дуги кривой

Читайте также:
  1. Вычисление скалярного произведения векторов через их координаты. Длина вектора. Угол между векторами.
  2. Длина волны в линии передачи
  3. Длина волны.
  4. Длина волос ТЗ от 3 см. Схема стрижки На НЗЗ – «дымчатый переход»
  5. Длина мертвой зоны
  6. Длина тел в разных системах отсчёта.
  7. Когерентные волны. Время и длина когерентности
  8. Корпускулярно-волновой дуализм. Длина волны де Бройля. Квантование электронных орбит атома в модели де Бройля. Соотношения неопределенностей.
  9. Местные сопротивления при ламинарном режиме течения. Эквивалентная длина.
  10. Механические волны. Свойства механических волн. Длина волны.
  11. Общая длина крепостных стен острога и башен Хотмышской крепости составляла 409 сажен (т.е. 850 м.).

Множество точек плоскости 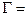с функциями будем называть непрерывной плоской кривой.

Пусть - некоторое разбиение отрезка . Обозначим через ломаную, которая получается соединением точек и , лежащих на кривой , отрезком прямой. Длина ломаной равна .

Определение 1. Если существует конечный предел , то кривая называется спрямляемой, а предел 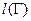называется длиной кривой .

Теорема 1. Пусть . Тогда кривая является спрямляемой, а ее длина равна .

Следствие 1 (Длина дуги в декартовых координатах). Если кривая L задана уравнением

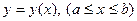, где , то ее длина

.


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.002 сек.)