Элементарные свойства интеграла

Установим ряд формул:

1) .

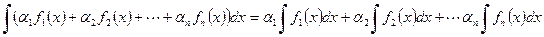Точный смысл этой формулы в том, что если 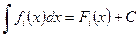, то

,

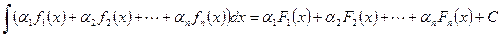(в частности 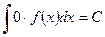). Это свойство называется линейностью неопределенного интеграла.

2) 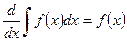– производная любой из функций, составляющих неопределённый интеграл , есть .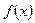

3) – в этой формуле записан тот очевидный факт, что одной из первообразных функции является .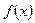

Пример1. Найти .

Решение. В этом примере

¶,

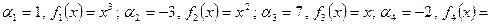где ¶, - функция, тождественно равная единице. Используя таблицу интегралов, находим 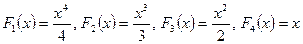. Применяем теперь формулу 1) и заключаем, что

.

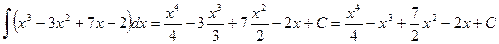Поиск по сайту: