АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Динамика переменной массы. Уравнение движения тела переменной массы. Уравнение Циолковского

Читайте также:
  1. Root(Выражение, имя переменной)
  2. А — при двустороннем движении судов; б — при одностороннем движения
  3. АЛГОРИТМ РЕШЕНИЯ ЗАДАЧ НА УРАВНЕНИЕ ТЕПЛОВОГО БАЛАНСА
  4. Анализ движения денежных средств прямым и косвенным методом
  5. Анализ движения и технического состояния основных средств
  6. Анализ движения основных фондов
  7. Анализ остатков и движения денежной наличности
  8. Анализ случаев нарушения безопасности движения с установлением виновных и конкретных нарушений правил и порядка работы
  9. В декартовых координатах каждая прямая определяется уравнением первой степени с двумя переменными и обратно: каждое уравнение первой степени
  10. В журнале движения больных отделения отмечаются сведения о движении больных: число выбывших и поступивших.
  11. Векторная величина — скорость, которой определяется как быстрота движения, так и его направление в данный момент времени.
  12. Взаимосвязь различных форм движения материи

 

Выведем уравнение движения тела переменной массы (например, движение ракеты сопровождается уменьшением ее массы за счет истечения газов, образующихся от сгорания топлива).
Пусть в момент времени t масса ракеты m, а ее скорость v; тогда по истечении времени dt ее масса уменьшится на dm и станет равной m–dm, а скорость увеличится до величины v+dv. Изменение импульса системы за время dt будет равно:



где u - скорость истечения газов относительно ракеты. Раскрывая скобки в этом выражении, получим:



Если на систему действуют внешние силы, то 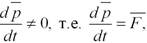или dp = Fdt. Тогда Fdt = mdv + udm, или

(2.12)

где член называют реактивной силой Fp. Если вектор u противоположен v, то ракета ускоряется, а если совпадает с v, то тормозится.
Таким образом, уравнение движения тела переменной массы имеет следующий вид:

(2.13)

Уравнение (2.13) называется уравнением И.В. Мещерского.
Применим уравнение (2.12) к движению ракеты, на которую не действуют никакие внешние силы. Тогда, полагая F = 0 и считая, что ракета движется прямолинейно (скорость истечения газов постоянна), получим:



откуда

 


или

 


где С – постоянная интегрирования, определяемая из начальных условий. Если в начальный момент времени v =0, а стартовая масса ракеты составляет m0, то C = u*ln m0. Следовательно,

(2.14)

Полученное соотношение называют формулой К.Э. Циолковского. Из выражения (2.14) следуют следующие практические выводы:
а) чем больше конечная масса ракеты m, тем больше должна быть стартовая масса m0;
б) чем больше скорость истечения газов u, тем больше может быть конечная масса при данной стартовой массе ракеты.
Уравнения Мещерского и Циолковского справедливы для случаев, когда скорости v и u намного меньше скорости света c.

 


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)