АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Дифференциальное уравнение затухающих колебаний

Читайте также:
  1. АЛГОРИТМ РЕШЕНИЯ ЗАДАЧ НА УРАВНЕНИЕ ТЕПЛОВОГО БАЛАНСА
  2. Амплитуда, период, частота, фаза колебаний.
  3. В декартовых координатах каждая прямая определяется уравнением первой степени с двумя переменными и обратно: каждое уравнение первой степени
  4. Введение в анализ и дифференциальное исчисление
  5. Внутреннее трение (вязкость) жидкости. Уравнение Ньютона
  6. Волна вероятности. Уравнение Шредингера
  7. Волновое уравнение и его решение. Физический смысл волнового уравнения. Скорость распространения волн в различных средах.
  8. Вопрос№15 Механические колебания. Виды колебаний. Параметры колебаний движения
  9. Временное и стационарное уравнение Шредингера. Решения.
  10. Вязкость жидкости. Уравнение Ньютона. Закон Пуазейля
  11. Гармонические колебания и их характеристики. Дифференциальное уравнение свободных гармонических колебаний.
  12. Гипербола. Каноническое уравнение гиперболы и его свойства.

Запишем второй закон Ньютона для пружинного маятника, в котором присутствует трение.

т = - k x – r ,

где F= - k x - возвращающая сила, линейная по смещению;

Fтр = - r - сила трения, линейная по скорости (знак минус свидетельствует, что она направлена в противоположную сторону скорости). Дифференциальное уравнение затухающих колебаний можно привести к виду

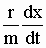+ =0,

Логарифмическим декрементом затухания

,

Ne — число колебаний, совершаемых за время уменьшения амплитуды в е раз. Логарифмический декремент затухания - постоянная для данной колебательной системы величина.


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.002 сек.)