Вопрос 5. Второй закон Ньютона можно записать в другой форме

Второй закон Ньютона можно записать в другой форме. Согласно определению:

,

тогда

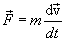или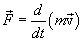

Вектор называется импульсом или количеством движения тела и совпадает по направлению с вектором скорости , а выражает изменение вектора импульса.

Преобразуем последнее выражение к следующему виду:

(3.6)

Вектор называется импульсом силы .

Это уравнение является выражением основного закона динамики материальной точки: изменение импульса тела равно импульсу действующей на него силы.

Используя уравнения:

и ,

можем записать

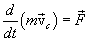
или

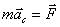
(3.12)

Таким образом, центр инерции механической системы движется как материальная точка, масса которой равна массе всей системы и на которую действует сила, равная главному вектору внешних сил, приложенных к системе. В общем случае движение твердого тела можно рассматривать как сумму двух движений: поступательного со скоростью , равной скорости центра инерции тела, и вращения вокруг центра инерции. Поэтому последнее уравнение часто называют основным уравнением динамики поступательного движения твердого тела.

Поиск по сайту: