 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Билет 31
|
Читайте также: |
| Первое начало термодинамики |
Молярной теплоемкостью C называется количество теплоты, которое необходимо передать 1 молю вещества, чтобы его температура увеличилась на 1 Кельвин:

|
В термодинамике широко используются понятия молярной теплоемкости при постоянном объеме CV и молярной теплоемкости при постоянном давлении Cp. В идеальном газе они удовлетворяют уравнению Майера:
| Cp – CV = R. |
Теплоемкость одного моля одноатомного идеального газа при постоянном объеме равна  , двухатомного –
, двухатомного –  , многоатомного – 3 R.
, многоатомного – 3 R.
Внутренняя энергия идеального газа прямо пропорциональна его абсолютной температуре:
| U = CVT. |
Работа Δ A, совершаемая газом, определяется давлением газа и изменением его объема:
| Δ A = p Δ V. |

|
| Рис. 1. Если давление газа в процессе совершения работы изменяется, то работа может быть найдена по площади под графиком |
|
| Рис. 2. Работа газа зависит от пути, по которому газ переходит из состояния 1 в состояние 2 |
Первое начало термодинамики. Количество теплоты, полученное системой, идет на изменение ее внутренней энергии и на совершение работы над внешними телами:
| Q = Δ U + A. |
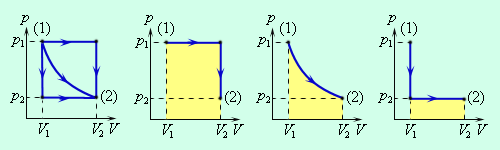
В изохорном процессе газ работы не совершает, и Δ U = Q. В изобарном процессе A = p Δ V = p (V 2 – V 1). В изотермическом процессе Δ U = 0, и A = Q; вся теплота, переданная телу, идет на работу над внешними телами. Графически работа равна площади под кривой процесса на плоскости p, V.

|
| Рис. 3. Первое начало термодинамики для изохорного процесса |

|
| Рис. 4. Первое начало термодинамики для изобарного процесса |

|
| Рис. 5. Первое начало термодинамики для изотермического процесса |

|
| Рис. 6. Первое начало термодинамики для адиабатного процесса |
Адиабатным называется квазистатический процесс, при котором системе не передается тепло из окружающей среды: Q = 0. В адиабатном процессе вся работа совершается за счет внутренней энергии газа.
32. При высоких давлениях и низких температурах модель идеального газа непригодна. Нужно учитывать силы межмолекулярного воздействия и объём самих молекул. Силы межмолекулярного воздействия – короткодейств. Они проявляются на расстояниях ~10-9 м (или меньше).
Между молекулами одновременно действуют силы притяжения и силы отталкивания.
Где-то, на расстоянии r0, в сумме они дают 0.
При r=r0 ƩF=0, r0 – равновесное состояние между молекулами.
Система из двух взаимодейств. молекул в состоянии устойчивого равновесия (r=r0) обладает min потенц. энергией. (Eп min)
Критерием различных агрегатных состояний вещ-ва явл-ся соотношение между Eп min и kT.
Eп min – наим. Потенц. энергия взаимодействия молекул – определяет работу, которую нужно совершить против сил притяжения для того, чтобы разъединить молекулы, находящиеся в равновесии (r=r0).
kT – удвоенна средняя кинетическая энергия, приходящаяся на одну степень свободы хаотического теплового движения молекул.
Если Eп min << kT – газообр.
Если Eп min >> kT – твёрдое.
Если Eп min  kT – жидкое.
kT – жидкое.
вывел ур-ие состояния реального газа:
Вандер-Ваальс ввёл 2 поправки:
1) Учёт собств. Объёма молекул. Реальный объём свободного движения молекул уменьш. на b (для Vν - b), где b – учетв. собств. Vмол, Vν – V1 моля
2) Учёт растяжения молекул. Действия сил притяжения газа приводит к появлению доп. давления на газ, называемого внутр. давлением.
p´=a/Vм2
Для 1 моля: (p+a/Vм2)(Vм-b)=RT
Ур-ие Вандер-Ваальса:
Только при высоких T и низких V.
Изотермы Вандер-Ваальса.
33. Круговой процесс (цикл) – процесс, в котором система, пройдя ряд состояний, возвращается в исходное.
Работа расширения равна площади под графиком.
a – расширение газа.
b – сжатие газа.
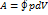 >0 – прямой цикл.
>0 – прямой цикл.
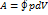 <0 – обратный цикл. Используется в холод.
<0 – обратный цикл. Используется в холод.
За цикл: ΔU=0, Q=A, Q=Q1-Q2=A
Термический КПД: 
Обратимый ТД процесс – процесс, который может происходить как в прямом, так и обратном направлении. При обратимом процессе не происходит никаких изменений. Необходимым и достаточным условием обратимости процесса является го равновесность. Любой равновесный процесс – обратимый. Пр.: адиабатическое расширение или сжатие, изотермическое расширение или сжатие.
Рассмотрение обратимых процессов важно про двум причинам
1. Многие процессы в природе и технике практически обратимы.
2. Обратимые процессы явл-ся экономически наиболее выгодными. Имеют максимальный термический КПД, что позволяет указать пути повышения КПД в реальных двигателях. (тепл.)
Необратимые процессы – процессы, сопровождающиеся диссипацией (рассеянием) энергии при теплообмене, расширение газа в пустоту.
34. Тепловым двигателем наз-ся устройство, в котором хаотическое движение молекул превращается в движение упорядоченное, иначе говоря, внутр. энергия превращается в механическую. Основная задача: превращение тепла в работу.
Цикл Карно: ΔS=  , если Q2<Q1
, если Q2<Q1  T2<T1
T2<T1
Холодильник+нагреватель+рабочее тело.
Рассм. Работе теплового двигателя.
Очевидно, что наибольшим КПД будет обладать ЦИК, состоящий из целиком обратимых процессов, при которых не происходит необр.переходов тепла от нагревателя к холодильнику с бесполезным увеличением энтропии.Основываясь на втором начале ТД, Карно вывел теорему:
Из всех периодически действ. машин, имеющих одинаковые T1 и T2 наиб. КПД обладают обратимые машины. При этом их ПД равны и не зависят от природы рабочего тела.

Схема цикла Карно в тетради (!).
35. Реальные тепловые процессы всегда необратимы. Существуют общие закономерности, указывающие направленность этих процессов. Эти закономерности связаны с качественными особенностями теплового движения. Качественным отличием теплового движения молекул от др. форм движения явл-ся хаотичность, беспорядочность.
Назовём макросостоянием системы состояние, определяющееся величинами, определяющими систему в целом.
P, V, T, U – макропараметры.
Микрососояние – состоянии макроскопического тела, при котором оказываются заданными состояния всех образующих тело микрочастиц.
 – микропараметры.
– микропараметры.
Всякое макросостояние может быть осуществлено различными способами, каждому из которых соответствуют некоторые микросостояния тела.
Термодинамическая вероятность (W) – число различных мероприятий, соответствующих данному макросостоянию.
Поясним это на примере распределения молекул газа в сосуде.
Вероятность нахождения одной молекулы в любой половине сосуда: 0,5.
Вероятность нахождения двух молекул: 0,25.
Вероятность нахождения трёх молекул: 0,125.
Всего возможно 24=16 различных распределений между двумя половинами объема сосуда. 16 – макросостояние.
При этом оказывается возможным 5 различных макрораспределений между двумя половинами сосуда.
В равновесном состоянии термодинамическая вероятность максимальна.
W=W1*W2*W3

1872 год – в качестве функции, характеризующей меру беспорядочности теплового движения, Больцман предположил взять величину 
S – энтропия системы – мера неупорядоченности системы или мера вероятности состояния данной системы.
Св-ва энтропии:
1) Энтропия изолированной системы при протекании необратимого процесса возрастает (т.е. система переходит из менее вероятного состояния в более вероятное). ΔS>0
2) В состоянии ТД равновесия – наиболее вероятного состояния – число микросостояний максимально, поэтому максимальна и энтропия.
3) Энтропия механических движений, которые всегда упорядочены = 0
4) Энтропия обладает свойствами аддитивности Sсистемы =S1+S2
5) Для обратимых процессов: ΔS=0
1865 г. – Клаузиус показал, что процесс превращения теплоты в работу подчиняется определенному закону (второе начало ТД).
Рассмотрим, как меняется энтропия при необратимых и обратимых процессах:
1. Необр.: Расширение газа в пустоту.
W~VN
2. Обр.:
Приведенное количество теплоты:
 – отношение количество теплоты, полученной телом в изотерм. процессе, к температуре теплоотдающего тела.
– отношение количество теплоты, полученной телом в изотерм. процессе, к температуре теплоотдающего тела.
Приведенное кол-во теплоты, сообщаемое телу в любом круговом процессе, равно 0.
 =0 – рав-во Клаузиуса. (3)
=0 – рав-во Клаузиуса. (3)
Под интегральным выражением есть полный дифференциал некоторой функции, которая определяется только состоянием системы и не зависит от пути, каким система пришла в это состояние.
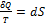 - энтропия функции состояния системы.
- энтропия функции состояния системы.
Если система совершает равновесный переход из состояния 1 в состояние 2, то изменение энтропии 
Физич. Смысл имеет не сама энтропия, а её производная.

1) T=const: 
2) V=const: 
3) 
Из рав-ва Клаузиуса 3 следует, что для обратимых процессов изменение энтропии равно 0.
 - в замкнутой системе.
- в замкнутой системе.
Энтропия либо возрастает для необр. процессов, либо остаётся постоянной для обр. процессов.
Второе начало ТД по Клаузиусу: невозможен круговой процесс, единственным результатом которого является передача теплоты от менее нагретого тела к более нагретому телу.
По Томсону: невозможен круговой процесс, единственным результатом которого является превращение теплоты, полученной от нагревателя, в эквивалентную работу (вечный двигатель второго рода невозможен).
О поведении ТД системы при 0 К говорит третье начало ТД.
Теорема Нернста-Планка: 

Энтропия всех тел в системе ТД равновесия
Поиск по сайту: