 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
IV Вычислить площадь фигуры
Перечень примеров для решения при подготовке к экзамену по курсу «Математика»
I Найти производную функции
1.1.  1.2.
1.2.  1.3.
1.3.  1.4.
1.4.  1.5.
1.5.  1.6.
1.6.  1.7.
1.7.  1.8.
1.8.  1.9.
1.9. 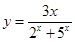 1.10.
1.10. 
| 1.11.  1.12.
1.12.  1.13.
1.13.  1.14.
1.14.  1.15.
1.15. 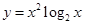 1.16.
1.16.  1.17.
1.17.  1.18.
1.18.  1.19.
1.19.  1.20.
1.20. 
| 1.21.  1.22.
1.22.  1.23.
1.23.  1.24.
1.24.  1.25.
1.25.  1.26.
1.26.  1.27.
1.27.  1.28.
1.28.  1.29.
1.29.  1.30.
1.30. 
|
II Найти неопределенный интеграл
2.1.  2.2.
2.2.  2.3.
2.3.  2.4.
2.4.  2.5.
2.5. 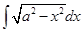 2.6.
2.6. 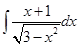 2.7.
2.7.  2.8.
2.8.  2.9.
2.9. 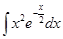 2.10.
2.10. 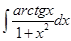
| 2.11.  2.12.
2.12.  2.13.
2.13.  2.14.
2.14.  2.15.
2.15.  2.16.
2.16.  2.17.
2.17.  2.18.
2.18.  2.19.
2.19. 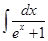 2.20.
2.20. 
| 2.21.  2.22.
2.22.  2.23.
2.23.  2.24.
2.24.  2.25.
2.25.  2.26.
2.26.  2.27.
2.27. 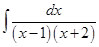 2.28.
2.28.  2.29.
2.29.  2.30.
2.30. 
|
III Вычислить определенный интеграл
3.1.  3.2.
3.2.  3.3.
3.3.  3.4.
3.4. 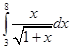 3.5.
3.5.  3.6.
3.6.  3.7.
3.7.  3.8.
3.8.  3.9.
3.9.  3.10.
3.10. 
| 3.11.  3.12.
3.12.  3.13.
3.13.  3.14.
3.14.  3.15.
3.15.  3.16.
3.16.  3.17.
3.17.  3.18.
3.18.  3.19.
3.19.  3.20.
3.20. 
| 3.21.  3.22.
3.22.  3.23.
3.23.  3.24.
3.24.  3.25.
3.25.  3.26.
3.26.  3.27.
3.27.  3.28.
3.28.  3.29.
3.29.  3.30.
3.30. 
|
IV Вычислить площадь фигуры
4.1.Найти площадь (S) каждой из фигур, на которые прямая y=x+4 делит фигуру, ограниченную линиями:

4.2.Найти площадь (S) фигуры, ограниченную параболой  и касательной к ней, проведенными через ее точки с абсциссами X=1 и X=3
и касательной к ней, проведенными через ее точки с абсциссами X=1 и X=3
4.3.Найти площадь (S) каждой из фигуры, ограниченную линиями 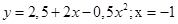 и касательной к данной параболе, проведенной через ее точку с абсциссой х=3
и касательной к данной параболе, проведенной через ее точку с абсциссой х=3
4.4.Вычислить площадь (S) фигуры, ограниченную линиями  сделать чертеж
сделать чертеж
4.5.Вычислить площадь (S) фигуры, ограниченную линиями  сделать чертеж
сделать чертеж
4.6.Вычислить площадь (S) фигуры, ограниченную линиями  сделать чертеж
сделать чертеж
4.7.Вычислить площадь (S) фигуры, ограниченную линиями  сделать чертеж
сделать чертеж
4.8.Вычислить площадь (S) фигуры, ограниченную линиями 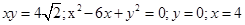
сделать чертеж
4.9.Вычислить площадь фигуры, ограниченную линиями 
4.10. Вычислить площадь (S) фигуры, ограниченную линиями 
сделать чертеж
4.11. Вычислить площадь (S) фигуры, ограниченную параболой  и гиперболой
и гиперболой 
сделать чертеж
4.12. Вычислить площадь (S) фигуры, ограниченную линиями 
4.13. Вычислить площадь фигуры, ограниченную линиями 
4.14. Найти площадь (S) фигуры, ограниченную линиями  , сделать чертеж.
, сделать чертеж.
4.15. Вычислить площадь (S) фигуры, ограниченную кривой  ,осью Оx и прямыми:
,осью Оx и прямыми: 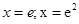 . Сделать чертеж
. Сделать чертеж
4.16. Вычислить площадь фигуры, ограниченную линиями:  сделать чертеж
сделать чертеж
4.17. Вычислить площадь (S) фигуры, ограниченную кривой  , прямыми:
, прямыми:  . Сделать чертеж
. Сделать чертеж
4.18. Построить площадь (S) фигуры, ограниченную кривыми: 
4.19. Построить площадь фигуры, ограниченную кривой 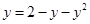 и осью ординат. Построить чертеж.
и осью ординат. Построить чертеж.
4.20. Вычислить площадь фигуры, ограниченную параболой 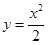 , прямыми
, прямыми  и осью абсцисс. Сделать чертеж.
и осью абсцисс. Сделать чертеж.
4.21. Определить площадь фигуры, ограниченной параболой  и прямой
и прямой  . Сделать чертеж.
. Сделать чертеж.
4.22. Найти площадь S области, ограниченной эллипсом 
4.23. Вычислить площадь фигуры, ограниченной линиями  . Сделать чертеж.
. Сделать чертеж.
4.24. Вычислить площадь фигуры, ограниченной линиями:  . Сделать чертеж.
. Сделать чертеж.
4.25. Найти площадь фигуры, ограниченной линиями:  . Построить чертеж.
. Построить чертеж.
4.26. Найти объем тела вращения вокруг оси ОХ фигуры, ограниченной линиями: 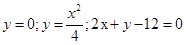 . Сделать чертеж.
. Сделать чертеж.
4.27. Найти площадь фигуры, ограниченной линиями:  .
.
4.28. Найти площадь фигуры, ограниченной линиями:  . Сделать чертеж
. Сделать чертеж
4.29. Найти площадь S фигуры, ограниченной линиями:  . Сделать чертеж
. Сделать чертеж
4.30. Вычислить площадь фигуры S, ограниченной осью ОХ и графиком функции  , при
, при  . Сделать чертеж
. Сделать чертеж
V Ряды
5.1. Разложить в ряд Маклорена функцию: 
5.2. Пользуясь разложением в ряд, приблизительно вычислить 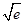 с точностью до
с точностью до  .
.
5.3.Разложить в ряд Маклорена функцию: 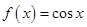
5.4.Разложить в ряд Маклорена функцию: 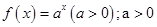
5.5.Представить в виде степенного ряда функцию: 
5.6.Представить в виде степенного ряда функцию: 
5.7.Разложить в ряд Тейлора функцию: 
5.8.Разложить в ряд Тейлора функцию: 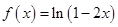
5.9.Разложить в ряд Тейлора функцию: 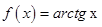
5.10. Вычислить 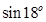 с точностью до 0,0001
с точностью до 0,0001
5.11. Вычислить  с точностью до 0,01
с точностью до 0,01
5.12. Вычислить 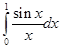 с точностью до 0,01
с точностью до 0,01
5.13. Разложить в степенной ряд функцию 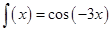
5.14. Разложить многочлен  по возрастающим степеням разности (x-2)
по возрастающим степеням разности (x-2)
5.15. Разложить в ряд Маклорена функцию 
5.16. Разложить в ряд Маклорена функцию 
5.17. Вычислить  с точностью до 0,0001
с точностью до 0,0001
5.18. Разложить в ряд Фурье периодическую функцию, заданную на полупериоде  уравнением
уравнением 
5.19. Разложить функцию,  по возрастающим степеням разности
по возрастающим степеням разности 
5.20. Исследовать необходимость ряда 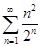
5.21. Разложить в тригонометрический ряд Фурье в интервале  функцию
функцию 
5.22. Разложить в тригонометрический ряд Фурье в интервале  функцию
функцию 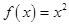
5.23. Разложить в ряд Тейлора функцию 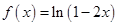
5.24. Разложить в тригонометрический ряд Фурье гиперболическую функцию 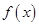 с периодом 2, заданную на сегменте
с периодом 2, заданную на сегменте  уравнением
уравнением 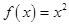
5.25. Выяснить сходимость ряда 
5.26. Выяснить сходимость ряда 
5.27. Разложить функцию,  на интервале
на интервале 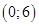 по синусам кратных дуг.
по синусам кратных дуг.
5.28. Пользуясь разложением в ряд  , вычислить
, вычислить 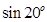 с точностью до 0,0001
с точностью до 0,0001
5.29. Разложить функцию  в ряд Тейлора в окрестности точки
в ряд Тейлора в окрестности точки 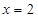
5.30. Разложить в степенной ряд функцию 
Поиск по сайту: