АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Для сферической поверхности

Читайте также:
  1. Дегазация — комплекс мероприятий, направленных на уничтожение (нейтрализацию) боевых отравляющих веществ или удаление их с зараженной поверхности.
  2. Дополнительные характеристики шероховатости поверхности.
  3. Касательная плоскость и нормаль к поверхности.
  4. Потенциальная энергия заряда. Эквипотенциальные поверхности.
  5. Уравнения упругих волн, плоской и сферической. Принцип суперпозиции волн. Фазовая и групповая скорости
  6. Формирование опорной поверхности.
  7. Эквипотенциальные поверхности. Связь между напряженностью и потенциалом

Пусть поле создается точечным электрическим зарядом q. Проведем замкнутую сферическую поверхность площадью S (рис. 2), окружающую этот заряд, центр которой совпадает с точкой нахождения заряда. Вычислим поток вектора напряженности через эту поверхность. За положительное направление нормали выберем направление внешней нормали . В этом случае во всех точках сферической поверхности E = const и cos α = 1.

Модуль напряженности поля на расстоянии R от заряда . Площадь поверхности сферы .

Следовательно, поток вектора напряженности через сферическую поверхность

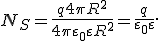
Полученный результат будет справедлив и для поверхности произвольной формы, а также при любом расположении заряда внутри этой поверхности. Действительно, если окружить сферу произвольной замкнутой поверхностью (рис. 2, а — поверхность изображена штрихами), то каждая линия напряженности, пронизывающая сферу, пройдет и сквозь эту поверхность.


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.002 сек.)