АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Условия на границе раздела двух диэлектрических сред

Читайте также:
  1. I. При каких условиях эта психологическая информация может стать психодиагностической?
  2. I. Психологические условия эффективности боевой подготовки.
  3. IV. ТРЕБОВАНИЯ К УЧАСТНИКАМ И ИХ УСЛОВИЯ ДОПУСКА
  4. VI ПРИЧИНЫ, УСЛОВИЯ И ВТОРЖЕНИЕ
  5. А) ОСНОВНЫЕ УСЛОВИЯ ВЕРНОЙ ПЕРЕДАЧИ СЛОВ, ОБОЗНАЧАЮЩИХ НАЦИОНАЛЬНО-СПЕЦИФИЧЕСКИЕ РЕАЛИИ
  6. АДАПТАЦИЯ И ОСНОВНЫЕ СПОСОБЫ ПРИСПОСОБЛЕНИЯ ЖИВЫХ ОРГАНИЗМОВ К ЭКСТРЕМАЛЬНЫМ УСЛОВИЯМ СРЕДЫ
  7. Анализ инвестиционных проектов в условиях инфляции
  8. Анализ ФСП основывается главным образом на относительных показателях, так как абсолютные показатели баланса в условиях инфляции сложно привести в сопоставимый вид.
  9. Аттестация рабочих мест по условиям труда
  10. БАЗИСНЫЕ УСЛОВИЯ КОНТРАКТА. ''ИНКОТЕРМС''.
  11. Базисные условия поставки товаров
  12. Билет 3. Назовите основные условия существования политической деятельности

Исследуем связь между векторами Е и D на границе раздела двух однородных изотропных диэлектриков (у которых диэлектрические проницаемости равны ε1 и ε2) при отсутствии на границе свободных зарядов.


 

Рис.1

 

Проведем вблизи границы раздела диэлектриков 1 и 2 небольшой замкнутый прямоугольный контур ABCDA длины l, с направлением ориентации, как показано на рис. 1. По теореме о циркуляции вектора Е, применительно к данному случаю

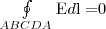
откуда

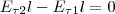
(знаки интегралов по АВ и CD разные, поскольку пути интегрирования противоположны, а интегралы по участкам ВС и DA малы). Поэтому

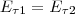(1)

Заменив проекции вектора Е проекциями вектора D, деленными на ε0ε, получим

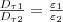(2)

построим прямой цилиндр ничтожно малой высоты на границе раздела двух диэлектриков (рис. 2); одно основание цилиндра находится в первом диэлектрике, другое — во втором. Основания ΔS настолько малы, что в пределах каждого из них вектор D одинаков. Согласно теореме Гаусса для электростатического поля в диэлектрике

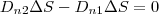
(нормали n и n' к основаниям цилиндра противоположно направлены). Поэтому

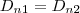(3)

Заменив проекции вектора D проекциями вектора Е, умноженными на ε0ε, получим

(4)

Значит, при переходе через границу раздела двух диэлектрических сред тангенциальная составляющая вектора Е (Еτ) и нормальная составляющая вектора D (Dn) изменяются непрерывным образом (не испытывают скачка), а нормальная составляющая вектора Е (Еn) и тангенциальная составляющая вектора D (Dτ) испытывают скачок.

Из условий (1) — (4) для составляющих векторов Е и D мы видим, что линии этих векторов испытывают излом (преломляются). Найдем как связаны между углы α1 и α2 (на рис. 3 α1>α2). Используя (1) и (4), Еτ2 = Еτ1 и ε2En2 = ε1En1. Разложим векторы E1 и E2 на тангенциальные и нормальные составляющие у границы раздела. Из рис. 3 мы видим, что

Учитывая записанные выше условия, найдем закон преломления линий напряженности Е (а значит, и линий смещения D)

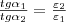
Из этой формулы можно сделать вывод, что, входя в диэлектрик с большей диэлектрической проницаемостью, линии Е и D удаляются от нормали.


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)