Бесконечная равномерно заряженная нить

Пусть τ — линейная плотность заряда нити. Выделим участок нити длиной Δ l и окружим его цилиндрической поверхностью, расположенной так, что ось цилиндра совпадает с нитью (рис. 5).

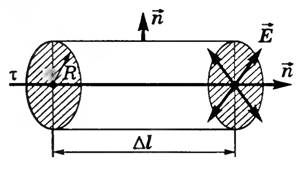
Рис. 5

Линии напряженности электростатического поля, создаваемого нитью в сечении, перпендикулярном самой нити, направлены перпендикулярно боковой поверхности цилиндра, поэтому поток напряженности сквозь боковую поверхность , где R — радиус цилиндра. Через оба основания цилиндра поток напряженности равен нулю (α = 90°, cos α = 0). Тогда полный поток напряженности через выделенный цилиндр

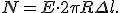
Заряд, находящийся внутри этого цилиндра, q = τ · Δ l.

Согласно теореме Остроградского—Гаусса, можно записать . Следовательно, модуль напряженности поля, создаваемого равномерно заряженной бесконечно длинной нитью на расстоянии R от нее,

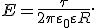
Поиск по сайту: