Вычисление непрерывных случайных величин

Непрерывная случайная величина h задана интегральной функцией распределения:

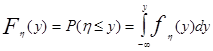, где 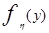- плотность вероятностей.

Для получения непрерывных случайных величин с заданным законом распределения, как и для дискретных величин можно использовать метод обратной функции. Взаимно однозначная монотонная функция h=F_h^-1(x), полученная решением относительно h управления F_h(y)=x преобразует равномерно распределённую на интервале (0,1) величину x в h с требуемой плотностью f­_h(y).

Действительно, если случайная величина h имеет плотность распределения f­_h(y), то распределение случайной величины является равномерным.

Т.о. чтобы получить число, принадлежащее последовательность случайных чисел {y}, имеющих функцию плотности f­_h(y), необходимо разделить относительно y_i управление

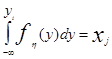(7)

Пример 2. Необходимо получить случайные числа y_i с показательным законом распределения.

f_h(y)=le^-ly, y>0.

В силу соотношения (7) получим 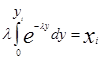, где x_i - случайное число, имеющее равномерное распределение в интервале (0,1), тогда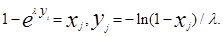

Рассмотрим универсальный метод моделирования непрерывных случайных величин (метод исключений).

При моделировании случайной величины y с плотностью распределения вероятностей f_h(y) в интервале a£y£b независимые значения x_m и x_m+1 преобразуются в значения

y_1m=a+(b-a)*x_m (8)

z_1m+1=f_1h(y)* x_m+1 (9)

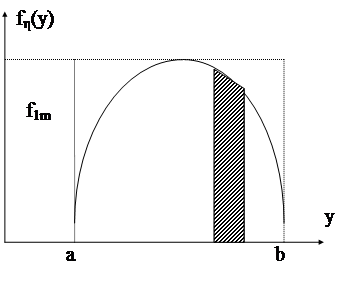
где f_1h(y)=max| f_h(y)|. При этом y_1m и z_1m+1 - значения случайных величин, равномерно распределенных на интервале (a,b) и (0,f_1m). Эти значения можно рассматривать как абсциссы и ординаты случайных точек, равномерно распределяющихся внутри прямоугольника со сторонами b-a и f_1m, охватывающего кривую распределения f_h(y) (см. рисунок 7.2.).

Рис. 7.2. Иллюстрация метода исключений

Если z_1m+1£f_h(y_m1), (10)

тогда пара y_1m, z_1m+1 определяет случайную точку под кривой f_h. Вероятность попадания случайной точки, удовлетворяющей условию (10) под кривую f_h равна единице, а вероятность попадания в заштрихованную элементарную площадку равна f_h(y_1m)*Dy_1m­. Это обозначает, что абсциссы y_1m случайных точек, попадающих под кривую f_h - значения случайной величины y с заданной плотностью вероятности f_h(y). Моделируемый алгоритм состоит из функций: 1) получения x_m1 и x_m+1 от датчика; 2) расчёта y_1v и z_1m+1 согласно (8) и (9); 3) вычисления f_h(y_1m); 4) сравнения z_1m+1 с f_h(y_1m). Если условия (10) выполняются, то y=y_1m; если нет, то значения y_1m и z_1m+1 исключаются и процесс повторяется, начиная с пункта 1. При моделировании системы 2-х случайных величин (y₁y₂) с плотностью вероятности f(y₁,y2), a₁£y₁£b₁; a₂£y2£b₂, аналогично моделированию одной случайной величины, три значения: x_m, x_m+1, x_m+2, выданные датчиком Е, преобразуются в значения:

y_1m=a₁+(b₁-a₁)x_m (11)

y_2m=a₂+(b₂-a₂)x_m+1 (12)

z_3m=f_hmx_m+2, где f_hm=max[f(x₁,x₂)] (13)

Если z_3m£f(y_1m,y_2m) (14)

то y₁=y_1m; y₂=y_2m.

В этом случае случайные точки с координатами y_1m, y_2m, z_3m - равномерно распределены в пределах параллепипеда со сторонами, равными (b₁-a₁)(b₂-a₂), f_hm и условие (14) означает попадание точки под поверхность f_h. Аналогично моделируется система n случайных величин (y₁,y₂,…,y_n).

Поиск по сайту: